SPACE:
Vacuum
or
Plenum –
the
Irony
of
Ancient
Atomism
per
‘Regenerism’.
Part 3. of the
Series on the
‘Regenerist
Hypothesis’.
Dear Reader,
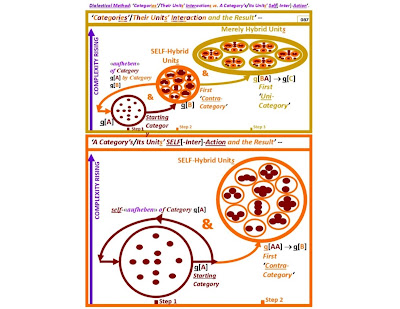
There is a kind of
philosophical, psychohistorical, ‘psychē-ic’, cognitive and ideational ‘«aufheben»
meta-«monads»-ization’ – i.e., a dialectic – in the relation between the
ancient Parmenidean universe-model of “BEING”, and the Leucippean, Democritean,
Epicurean and Lucretian universe-model of “atoms and the void”.
We are addressing ancient
philosophical ideologies here –
Parmenideanism and Atomism – yet
their discussion here bears upon contemporary times as well, for ideologies deeply
influenced by and akin to Parmenideanism and Atomism still figure prominently
in the unscientific, ideological biases of many present-day scientists,
especially many “particle physicists” and “social-atomist” economists.
Parmenides’s universe, of “being”,
was supposed to be a ‘‘‘substance’’’, one which is entirely homogeneous,
immutable, eternal, statical, and organized as a sphere, in the form of
a single, part-less. universal, unmodifiable unity.
Hence, all human sensuous
perception of qualitative difference, differentiation, movement, and
change-in-general, is mere delusion per Parmenides.
The atomists’ worldview, on
the contrary, posits a vast multiplicity of invisibly tiny, moving and colliding
units that are “uncuttable” [Gr. «a-tom-on»]
– “indivisible”, with the ‘«a-»’ serving as
a negatory prefix.
However, these “a-toms”,
or “not-toms” [cf. “tom-o-graph-y”]
are also, each one in its own right, “entirely part-less, homogeneous,
immutable, eternal, and statical internally”.
Thus, we may see that the “atoms”
of Democritus, et al., are, each one, somewhat like a tiny ‘Parmenideanoid’
“sphere”, although they interact/collide with one another, and move, mechanically,
externally, eternally.
Thus the Democritean, etc., ontological
category-unit for our universe as a whole can be grasped as an «arithmos»
that is made up out of a vast number, a [somewhat] heterogeneous gargantuan multiplication
of Parmenidean “Being”(s) as its «monads», deriving, by an
«aufheben»-negation, a determinate-negation/-elevation/conservation, of
the single “Being” unit(y) of the Parmenidean “singleton” ontological
category for our universe, the latter thus not an «arithmos»
in the ancient Greek sense, because it involves only one unit(y)/«monad». One unit did not a “quantity”
make, was not a “number”, per the ancient Mediterranean «arithmos» theory,
and its «arithmêtikê».
The Atomists’ universe, as a
single unit in its own right, was, in effect, made up out of a heterogeneous
multiplicity of the single unit that constituted the Parmenidean universe, by
means of a vast multiplication/replication-with-difference of that Parmenidean
universe unit.
With the Parmenidean
singleton-category model of our universe, as the ‘«arché»-category’,
and the high-multiplicity of «monads» of the Atomists’ «arithmos»
ontological category as ‘first contra-category’, we might wonder if there can
be a synthesis of these two ontological categories; their ‘first uni-category’.
However, we will leave that question unaddressed here, because we need to address another feature of the Atomists’
universe-model, also a ‘contra-Parmenidean’ feature. For the Atomists did not
just ontologically posit “atoms”, ‘contra-Parmenidean’ by virtue of their
multiplicity and their external, mechanical movement.
They posited atoms and
the void.
The “void” was conceived as a
mere ‘‘‘substance-less’’’ nothingness, an opposite to each and every, ‘substance-full’,
“atom”, and ‘anti-atom’ whose only virtue was to separate the atoms so that
they could be; could be “atoms”; could be distinct from
one another, and thus form a multiplicity.
Parmenides abhorred
the very notion of “nothingness”. He
would not countenance his “BEING” having any other;
any opposite.
The irony of the
ancient Atomists’ ‘voidism’, from the point of view of our ‘Regenerist Hypothesis’, is that, per this
hypothesis, “atoms” in the modern sense – quite cuttable – and the “particles”
into which they can be “cut”, and, maybe also, the, still unknown, units or «monads»
of “Dark Matter”, come from physical space, come from the supposed “vacuum”
of that space, evacuated of all “atoms”, of all “substance(s)”; they
all come from the Atomists’ “void”; in fact were generated by their
so-called “void”.
Per the ‘Regenerist
Hypothesis’, the physical space of our cosmos is a “plenum”, a ‘flowing
fullness’, not an “emptiness”; not a “vacuum”
at all!
And that ‘[out-]flowing
fullness’ is what the physicists and cosmologists are calling “Dark Energy”.
Per Hypothesis, our physical space is in reality a ‘plenum of replitrons’, or of ‘spandetrons’, that constitute “Dark Energy” – an all-pervading substance, but a substance that our Darwinianly-adapted sensoria are not equipped to detect, but that we have detected, by means of complex instruments and calculations that extend our senses, beyond our genome, via our ‘‘‘phenome’’’, albeit only quite recently, only yesterday, via very difficult-to-make measurements, that reveal the self-accelerating self-expansion of universal space – a phenomenon that mainstream physics and cosmology never even considered, theoretically, conceptually, until it was thrust upon them by empirical observation.
However, it would be
premature to conclude that our
hypothetical ‘spandetron’/‘replitron’ «monads» are “the a-toms of space”
– are “a-toms” in the ancient sense of being [the ultimate] “uncutables”; the
ultimate “elementary particles”, because
we still know so little about “Dark Energy” as of the present time.
For more
information regarding these
Seldonian insights, and to read and/or download, free
of charge, PDFs and/or JPGs of Foundation books, other texts, and images, please see:
and
https://independent.academia.edu/KarlSeldon
For partially pictographical, ‘poster-ized’ visualizations of many of these Seldonian insights -- specimens of ‘dialectical art’ – as well as dialectically-illustrated books
published by
the F.E.D. Press, see –
https://www.etsy.com/shop/DialecticsMATH
¡ENJOY!
Regards,
Miguel
Detonacciones,
Voting Member, Foundation Encyclopedia Dialectica [F.E.D.];
Elected Member, F.E.D. General Council;
Participant, F.E.D. Special Council for Public Liaison;
Officer, F.E.D. Office of Public Liaison.
YOU are invited to post
your comments on this blog-entry below!
