[Note: This topic will also be continued further in my next blog entry].
space --
NB = { b/1, b/2, b/3, b/4, . . .} = { b1, b2, b3, b4, ...}.
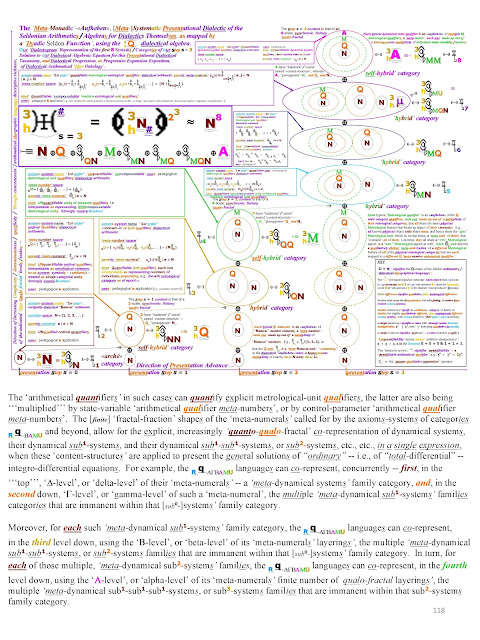
It seems to me that many of the systems of dialectical arithmetic in this "meta-system-atic" systems-progression are strictly presentational / pedagogical / illustrative in character, in terms of presenting, step-by-step, all of the discrete steps necessary to the construction of the dialectical arithmetics that are more useful in scientific [meta-]modeling applications.
The more useful dialectical arithmetics tend to be either the R-based, or "Real" Numbers based, "quanto-qualitative" "full uni-thesis", or "grand synthesis", dialectical-arithmetical systems, which use R [---) q/1 as their <<arche'>>, rather than N, such as the --
q/3 (---] RU_
-- or the --
q/7 (---] Rq/MU
-- or the --
q/15 (---] Rq/AMU
systems, in the R-parallel portion of that systems-progression "explicitized" above, or such as the pure-qualitative systems of dialectical arithmetic, e.g., the N-based --
q/24 (---] Nq/BA
[example(s) in use -- http://www.dialectics.info/dialectics...AY2008_OCR.pdf -- slide 7],
-- or the --
q/56 (---] Nq/GBA
[example(s) in use -- http://www.dialectics.info/dialectics...AY2008_OCR.pdf -- slide 35]
-- or the --
q/120 (---] Nq/DGBA
[example(s) in use -- http://www.dialectics.info/dialectics...AY2008_OCR.pdf -- slides 10 through 11]
-- systems of dialectical arithmetic, which can explicitly model trans-Platonian, human-phenomic <<arithmoi eidetikoi>> dialectical systematizations, with, e.g., two explicit levels of "ideo-taxonomy" [Nq/BA], three explicit levels of "ideo-taxonomy" [Nq/GBA], or four explicit levels of "ideo-taxonomy" [Nq/DGBA], etc., wherein "A" stands for the first Greek [capital] letter, "Alpha", "B" for the second Greek [capital] letter, "Beta", "G" for the third Greek [capital] letter, "Gamma", and "D" for the fourth Greek [capital] letter "Delta", in [Greek] alphabetical order.
TO BE CONTINUED . . .
Regards,
Miguel