Thought it might be useful to reproduce here the core "axioms" -- the main rules -- of the "rules-system" of the Seldonian "First Dialectical Arithmetic".
In this post, I am basing my account on the following F.E.D. writings --
http://www.dialectics.info/dialectics/Correspondence.html
http://www.dialectics.info/dialectics/Correspondence_files/Letter17-06JUN2009.pdf
http://www.dialectics.info/dialectics/Dialectic_Ideography.html
http://www.dialectics.info/dialectics/Dialectic_Ideography_files/6_Dialectics-Part1c-Briefing_OCR.pdf
[pages I-144 through I-150 especially].
http://www.dialectics.info/dialectics/Primer.html
http://www.dialectics.info/dialectics/Primer_files/3_F.E.D.%20Intro.%20Letter,%20Supplement%20A-1_OCR.pdf
[pages A-1 through A-35].
These eleven dialectical-arithmetical rules, or axioms, are rendered below in a language closer to everyday English -- less in the language of symbolic logic than in the sources cited above, or in my immediately-previous post to this thread, and with some commentary from yours truly.
Throughout, I am using visible-light-spectrum-order color-coding -- red, orange, yellow, green, blue, indigo, violet -- to call attention to relative, dialectical, qualitative ordinality.
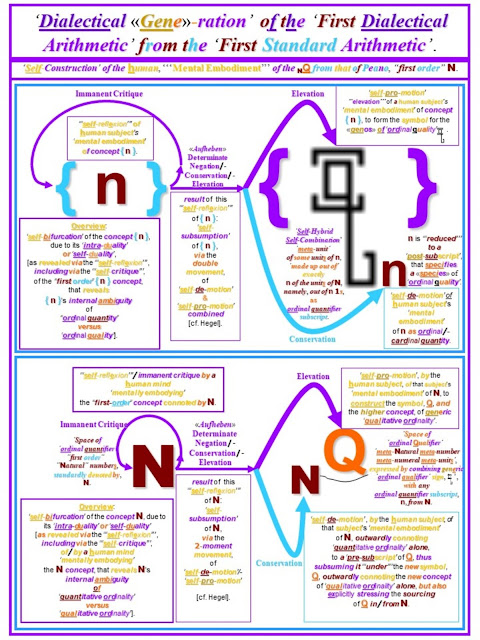
The "Peano Postulates" are the Standard axioms for the Standard Natural Numbers, the "set" or "space" N = {1, 2, 3, . . . }.
An arithmetic that follows these postulates, yet is qualitatively different from the Standard Natural Numbers, is called a "Non-Standard Model" of the Peano Postulates.
Such "Non-Standard Models" have been relatively little explored in academic mathematics.
Such a "Non-Standard Model" is the F.E.D. "First Dialectical Arithmetic", whose "meta-number" space they denote by NQ = { q/1, q/2, q/3, . . . }.
A key concept for the "Peano Postulates" is that of the successor function, which, for the N, can be expressed, for all n in N, as s(n) = n + 1.
The successor function for NQ incorporates the function s in its own version of the successor function, denoted by s:
s[q/n] = q/(s(n)) = q/(n+1).
1. q/1 is an element of NQ. [this is the NQ Non-Standard version of Peano Postulate # 1]
2. For any n in N, if q/n is in NQ, then s(q/n) = q/(n+1) is in NQ as well. [i.e., the successor of any element of NQ is also an element of NQ].
[this is the NQ version of Peano Postulate # 2].
3. For any j and k, both in N: If q/j is not equal to q/k, then the successor of q/j is not equal to the successor of q/k. [i.e., no two, distinct elements of NQ have the same successor].
[this is the NQ version of Peano Postulate # 3].
4. For all x in N: There is no q/x in NQ such that the successor of q/x is q/1. [i.e., q/1 has successors in NQ, but has no predecessor(s) in NQ; q/1 is the "arche'" of the NQ "meta-numbers"]. [this is the NQ version of Peano Postulate # 4].
5. For every n in N, q/n is in NQ. [this states the "aufheben" tie between the N and the NQ. The rest of the rules below state "Non-Standard" aspects of the NQ relative to the "Standard" N].
6. For any j and k, both in N: If j is quantitatively unequal to k, then q/j is qualitatively unequal to q/k.
[This axiom expands the "trichotomy principle" of the "Standard" arithmetics -- the principle that for any arithmetical objects a and b, just one of the following three relations obtains:
a < b, or a = b, or a > b
-- to a "tetrachotomy principle", that adds a fourth possibility, that of qualitative inequality, to the basic possible relations between any pair of arithmetical objects].
7. For all n in N: q/n + q/n = q/n.
[the kind of "addition of likes" specified by this rule is called "idempotent addition". It is true not only for the NQ dialectical logic, but also for the modern Boolean algebra of formal logic, in which not only does 0 + 0 = 0, but also 1 + 1 = 1. In the context of dialectically interpreted NQ expressions, it means that repeated "summed" occurrences of the same ontological category symbol is redundant, i.e., per our previous post, C + C = C, not "2C". This is the rule that makes the NQ arithmetic "non-quantitative", or "purely qualitative". The "count" of the presence(s) of any ontological category symbol can never exceed "1". This rule is crucial to the calculations summarized in that previous post].
8. For all j, and k, both in N:
If j is quantitatively unequal to k, then
q/j + q/k is qualitatively unequal to q/x
for any x in N.
[This is the rule that makes dialectically interpreted NQ expressions "ontologically anti-reductionist". It means that a "heterogeneous sum" of ontological categories, like C + M in the previous post, does not reduce or collapse into any single ontological category at the same level of generalization as its summands. This rule too is crucial to the calculations summarized in that previous post].
9. For every j and k, both in N: [q/k] x [q/j] = [q/j] + [q/(k+j)].
[This rule is most crucial of all to the "purely-qualitative, algorithmic calculations" presented in the previous post. It defines what "[ontological] multiplication" means among the NQ "dialectical meta-numbers". It is called, by F.E.D., "the double-aufheben evolute product rule".]
10. For all j, and k, both in N:
q/j + q/k = q/k + q/j
[This rule -- the commutative "law" of addition -- is shared, by the NQ dialectical arithmetic, with most of the more familiar "Standard" arithmetics. The indifference of the value of an NQ "qualitative sum" to the order of its terms does not mean, however, that there is not a preferred order for sums of NQ "meta-numbers" / "dialectors". That preferred order -- the "progressive order" -- is their "ordinal order":
q/1 + q/2 + q/3 + q/4 + q/5 + q/6 + q/7 + q/8 + . . .]
11. For all i, j, and k, all in N:
[ q/i + q/j ] + q/k = q/i + [q/k + q/j ]
[This rule -- the associative "law" of addition -- is shared, by the NQ dialectical arithmetic, with most of the more familiar "Standard" arithmetics.]
Extended Commentary.
This product rule is called "double aufheben", I think, because the j denominator/subscript of the "multiplicand" or "operand", q/j, is "aufheben-conserved" twice, in both the first, "Boolean", term of the product, and, once again, in the second, "ontology-increment" term of the product, where it is also, simultaneously "aufheben-negated/determinately-changed" and "aufheben-elevated", by the addition, to that j denominator/subscript, of the k denominator/subscript from the "multiplier" or "operator", q/k.
This product rule is called "evolute" because it encodes, in generic syntax, an empirical observation of great generality: when a new, higher level of organization irrupts within a given universe[-of-discourse], not all still-extant units [if any, if not completely "extincted"] of the previously-irrupted levels of organization are converted into units of the new level [as they would be in "convolute product-tion"]. Some of the previous levels' units remain unconverted to the new, higher level units.
E.g., not all Commodity units disappear / are converted into Money units, once the concentrated ferment of Commodity-barter reaches the quantitative threshold where qualitative/ontological change irrupts; where the new, previously-unprecedented units of Money-Commodit(y)(ies) irrupt, forming the next <<arithmos>> [assemblage-of-units] of social-relations-of-production human-social ontology. Units at the Commodity level of organization remain present, "even" after the "Money-ontology revolution" irrupts in any locus of human history.
E.g., not all atoms disappear / are converted into molecules, once the concentrated ferment of atoms-formation reaches the quantitative threshold where qualitative/ontological change irrupts; where the new, previously-unprecedented units called "molecules" irrupt, forming the next <<arithmos>>-of-<<monads>> [assemblage-of-units of cosmological, dialectic-of-nature ontology]. Units at the atom level remain present, "even" after the "molecules-ontology revolution" irrupts in any locus of cosmological natural history; of the "meta-evolution" of the cosmos.
In the Boolean algebra for formal logic, x times x = x, e.g., 1 times 1 = 1, and 0 times 0 = 0.
In fact, Boole called this rule "the fundamental law of [undialectical] thought".
The "Boolean term" is still there in this rule 9., for F.E.D. dialectical logic.
The "multiplicand", q/j, returns in the "aufheben" product.
That is a part of the "aufheben" operation: a "conservation" moment.
However, this rule for dialectical logic not only includes but also goes beyond that for formal logic in adding a second term -- a term that simultaneously "conserves, determinately changes/negates, and elevates" the "multiplicand", or "operand", q/j.
That second term, qualitatively distinct from q/j, per Rule 6., and capable of representing the "aufheben" revolutionary irruption of new ontology, of a new ontological category, is q/(k+j), which still "contains"/"conserves" j in its denominator, but, also, adds k to it, thereby also changing / determinately "negating" and "elevating" that denominator vis-a-vis that of q/j.
If a q/j -- say q/1 -- is "interpreted" for, or "assigned" to, a specific ontological category, for example, to C, denoting the Commodities <<arithmos>> of <<monads>> [ = assemblage of Commodity units], then --
[q/1] x [q/1] = [q/1] + [q/(1+1)] = q/1 + q/2
-- stands for the "interpreted" dialectical-ontological process --
C x C = [q/C] x [q/C] = [q/C] + [q/CC] = [q/C] + [q/M] = C + M.
The "interpreted" expression can be read as --
"the self-reflexion / self-confrontation / self-operation of a sufficiently numerous and spatially-concentrated "population" of Commodities continues to expandedly-reproduce itself, but also <<aufheben>>-irrupts a new ontological category/<<arithmos>>/"population": that of "Monies"; an assemblage of a new kind of units; whose units are Money units".
Each unit of Money is, in the minds of the human agents of the Money-social-relation-of-production, a meta-Commodity unit.
Each unit of Money, as meme, is made up out of a heterogeneous multiplicity of the Commodities that Money will trade-for, a mental "Money-price-list" for the various purchasable Commodities, a la the lists in "value-form" sections C. and D. in Chapter I. of Volume I. of Marx's Capital.
Another example: Assigning q/4 to the ontological category "atoms", denoted a, in an NQ model of the dialectic of nature, then we have --
[q/4] x [q/4] = [q/4] + [q/(4+4)] = [q/4] + [q/8]
-- standing for the "interpreted" dialectical-ontological process --
a x a = [q/a] x [q/a] = [q/a] + [q/aa] = [q/a] + [q/m] = a + m.
The "interpreted" expression can be read as --
-- "the self-reflexion / self-confrontation / self-operation of a sufficiently numerous and sufficiently spatially-concentrated, or "self-densified", "population" of atoms continues to expandedly-reproduce itself, but also aufheben-irrupts a new ontological category/"arithmos"/"population": that of "molecules"; the assemblage of a new kind of unit, the irruption of a new kind of assemblage, whose units are molecules".
Each typical molecule unit is a meta-atom.
Each typical molecule unit is made up out of a heterogeneous multiplicity of its predecessor units, atom units.
Regards,
Miguel
F.E.D. definitions for special terms applied in the narrative above --
<<arithmos>>
http://www.point-of-departure.org/Point-Of-Departure/ClarificationsArchive/Arithmos/Arithmos.htm
<<aufheben>>
http://www.point-of-departure.org/Point-Of-Departure/ClarificationsArchive/Aufheben/Aufheben.htm
convolute
http://www.point-of-departure.org/Point-Of-Departure/ClarificationsArchive/Convolute/Convolute.htm
evolute
http://www.point-of-departure.org/Point-Of-Departure/ClarificationsArchive/Evolute/Evolute.htm
[the] dialectic of nature
no definition is as yet available in the Clarifications Archive, but see pp. B-20 through B-22 in --
http://www.dialectics.info/dialectics/Primer_files/4_F.E.D.%20Intro.%20Letter,%20Supplement%20B-1,%20v.2_OCR.pdf
dialectical meta-numbers
no definition is as yet available in the Clarifications Archive
dialectical logics
http://point-of-departure.org/Point-Of-Departure/ClarificationsArchive/DialecticalLogics/DialecticalLogics.htm
formal logics
http://point-of-departure.org/Point-Of-Departure/ClarificationsArchive/Logics/Logics.htm
<<meme>>
no definition is as yet available in the Clarifications Archive
ontological reductionism, and [ontological] anti-reductionism
no definition is as yet available in the Clarifications Archive
ontological category
http://www.point-of-departure.org/Point-Of-Departure/ClarificationsArchive/Onto/Onto.htm
ontology
http://point-of-departure.org/Point-Of-Departure/ClarificationsArchive/Ontology/Ontology.htm
[neo-]ontology-increment term
no definition is as yet available in the Clarifications Archive
[dialectical, qualitative] ordinality
no definition is as yet available in the Clarifications Archive
purely-qualitative
no definition is as yet available in the Clarifications Archive
units [<<monads>>]
http://www.point-of-departure.org/Point-Of-Departure/ClarificationsArchive/Monad/Monad.htm



No comments:
Post a Comment