Comparison:
The Dialectic of Algebraic Formal Logic
versus
The Dialectic of '''Whole numbers''' Arithmetic
Dear Reader,
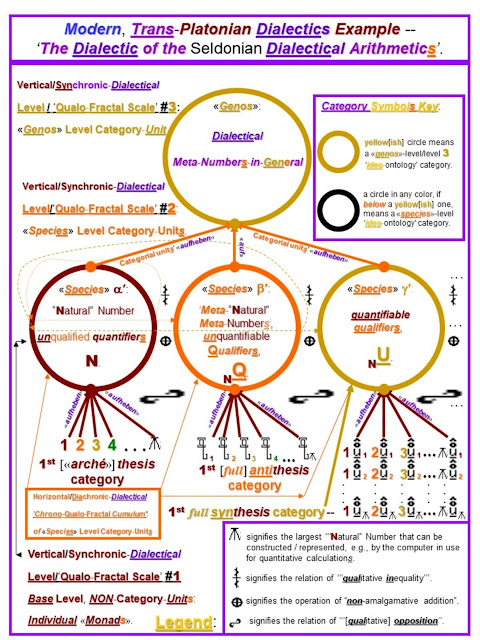
The foci of this post are two F.E.D. "dialectical equations", both of which are expressed in the "ideo-graph-ical language" of the algebra of their NQ_ "First Dialectical Arithmetic".
The first of the two dialectical equations expresses the dialectical elaboration of the "Boolean" algebra of formal logic as <<arche'>>.
The second of the two dialectical equations expresses the dialectical elaboration of the "Peanoian" "natural" axiomatic arithmetic of "unqualified quantifiers", the "number-space" of the Whole numbers --
W...=...{0, 1, 2, 3, . . . }
-- as <<arche'>>.
Per the F.E.D. "solution" -- or "semantification" -- for the two post-<<arche'>> terms of both of these two equations, the categorial-progressions, or axioms-system progressions, that these equation generate both converge and intersect in an in-common second, "contra-system" term, which connotes the axioms-system of the W-based arithmetic of pure, unquantifiable ontological/categorial qualifiers --
WQ_
-- whose space of "meta-numbers" is --
WQ...=...{q/0, q/1, q/2, q/3, . . . }.
When a "meta-numeral" -- generically, call it x -- is "underscored", or underlined, as are the qs in the q/n above, except for q/0, then, per the F.E.D. Encyclopedia Dialectica notation, this signifies that the "meta-number" thus notated exhibits the "contra-Boolean" characteristic", i.e., that this "meta-number", as "self-function", i.e., when it operates upon itself, e.g., when it is self-multiplied, or "squared", produces, as its "self-product", a value which is qualitatively unequal to its "unsquared" value, viz. --
x^2...=...xx...=...x(x) is not greater than & is not equal to & is not less than x
-- whereas, for a non-underscored [meta-]number, i.e., for a "Boolean" [meta-]number, generically denoted by x --
x^2...=...xx...=...x(x) is greater than OR is equal to OR is less than x.
For F.E.D.'s exposition of the centrality of this "not-not-not" -- or "neti-neti-neti" -- relation that characterizes their dialectical "meta-numbers" -- this relationship of "non-quantitative inequality", or of "qualitative inequality" -- and its ubiquity, and the relation-sign that they "coined" for it, and the revolution in mathematics implied by its transcendence of the mathematical "trichotomy principle", and its supercession by their dialectical-mathematical "tetrachotomy principle", see --
http://www.dialectics.info/dialectics/Primer_files/3_F.E.D.%20Intro.%20Letter,%20Supplement%20A-1_OCR.pdf
Unlike F.E.D., which uses the Dyadic Seldon Function equations to express both of these dialectical axioms-systems progressions, I will use the Triadic Seldon Function equations, for step s..=..1, to express these dialectical axioms-systems progressions, in order to focus attention on the first three terms/systems of each systems progression only.
Specifically, the two equations in question are the following --
(WE_)^(3^1)......=.....?
-- and --
(W_)^(3^1)......=......?
-- wherein WE_ connotes the "Elector" algebra of the "Boolean" axiomatic arithmetic system for algebraic formal logic, whose space is WE...=...{0, 1}, and wherein W_ connotes the "Peanoian" "Whole Number" axiomatic system of arithmetic, whose space is --
W...=...{0, 1, 2, 3, . . . }.
The general, s-as-variable form of the first of our two "dialectical equations" --
(WE_)^(3^s)......=.....?
-- asks the question "What new axioms-systems follow, dialectically, from the premise/<<arche'>> of the "Boolean" axioms-system of "quasi-quanto-qualitative" algebraic formal logic?".
The general, s-as-variable form of the second of our two "dialectical equations" --
(W_)^(3^s)......=......?
-- asks the question "What new axioms-systems follow, dialectically, from the premise/<<arche'>> of the "Whole Number" axioms-system of "purely-quantitative", "Peanoian/Natural" arithmetic?".
For step s..=..1, F.E.D.'s answers to these question/solutions to these equations -- their "semantification" of, or "meaning-discovery" for, the two new terms generated in each case -- is as follows.
Exercising the generic "self-combination" rules for the expansion of these Triadic Seldon Function equations, to obtain their still specifically unsolved generic expressions, we have --
The Dialectic of Algebraic Formal Logic
versus
The Dialectic of '''Whole numbers''' Arithmetic
Dear Reader,
The foci of this post are two F.E.D. "dialectical equations", both of which are expressed in the "ideo-graph-ical language" of the algebra of their NQ_ "First Dialectical Arithmetic".
The first of the two dialectical equations expresses the dialectical elaboration of the "Boolean" algebra of formal logic as <<arche'>>.
The second of the two dialectical equations expresses the dialectical elaboration of the "Peanoian" "natural" axiomatic arithmetic of "unqualified quantifiers", the "number-space" of the Whole numbers --
W...=...{0, 1, 2, 3, . . . }
-- as <<arche'>>.
Per the F.E.D. "solution" -- or "semantification" -- for the two post-<<arche'>> terms of both of these two equations, the categorial-progressions, or axioms-system progressions, that these equation generate both converge and intersect in an in-common second, "contra-system" term, which connotes the axioms-system of the W-based arithmetic of pure, unquantifiable ontological/categorial qualifiers --
WQ_
-- whose space of "meta-numbers" is --
WQ...=...{q/0, q/1, q/2, q/3, . . . }.
When a "meta-numeral" -- generically, call it x -- is "underscored", or underlined, as are the qs in the q/n above, except for q/0, then, per the F.E.D. Encyclopedia Dialectica notation, this signifies that the "meta-number" thus notated exhibits the "contra-Boolean" characteristic", i.e., that this "meta-number", as "self-function", i.e., when it operates upon itself, e.g., when it is self-multiplied, or "squared", produces, as its "self-product", a value which is qualitatively unequal to its "unsquared" value, viz. --
x^2...=...xx...=...x(x) is not greater than & is not equal to & is not less than x
-- whereas, for a non-underscored [meta-]number, i.e., for a "Boolean" [meta-]number, generically denoted by x --
x^2...=...xx...=...x(x) is greater than OR is equal to OR is less than x.
For F.E.D.'s exposition of the centrality of this "not-not-not" -- or "neti-neti-neti" -- relation that characterizes their dialectical "meta-numbers" -- this relationship of "non-quantitative inequality", or of "qualitative inequality" -- and its ubiquity, and the relation-sign that they "coined" for it, and the revolution in mathematics implied by its transcendence of the mathematical "trichotomy principle", and its supercession by their dialectical-mathematical "tetrachotomy principle", see --
http://www.dialectics.info/dialectics/Primer_files/3_F.E.D.%20Intro.%20Letter,%20Supplement%20A-1_OCR.pdf
Unlike F.E.D., which uses the Dyadic Seldon Function equations to express both of these dialectical axioms-systems progressions, I will use the Triadic Seldon Function equations, for step s..=..1, to express these dialectical axioms-systems progressions, in order to focus attention on the first three terms/systems of each systems progression only.
Specifically, the two equations in question are the following --
(WE_)^(3^1)......=.....?
-- and --
(W_)^(3^1)......=......?
-- wherein WE_ connotes the "Elector" algebra of the "Boolean" axiomatic arithmetic system for algebraic formal logic, whose space is WE...=...{0, 1}, and wherein W_ connotes the "Peanoian" "Whole Number" axiomatic system of arithmetic, whose space is --
W...=...{0, 1, 2, 3, . . . }.
The general, s-as-variable form of the first of our two "dialectical equations" --
(WE_)^(3^s)......=.....?
-- asks the question "What new axioms-systems follow, dialectically, from the premise/<<arche'>> of the "Boolean" axioms-system of "quasi-quanto-qualitative" algebraic formal logic?".
The general, s-as-variable form of the second of our two "dialectical equations" --
(W_)^(3^s)......=......?
-- asks the question "What new axioms-systems follow, dialectically, from the premise/<<arche'>> of the "Whole Number" axioms-system of "purely-quantitative", "Peanoian/Natural" arithmetic?".
For step s..=..1, F.E.D.'s answers to these question/solutions to these equations -- their "semantification" of, or "meaning-discovery" for, the two new terms generated in each case -- is as follows.
Exercising the generic "self-combination" rules for the expansion of these Triadic Seldon Function equations, to obtain their still specifically unsolved generic expressions, we have --
(WE_)^(3^1)......=
WE_..+..Wq/EE_..+..Wq/EEE_
-- and --
(W_)^(3^1)......= ......
W_..+..q/WW_..+..q/WWW_.
The F.E.D. solution, or "semantification", for the first equation's second and third terms is based upon the following overall intuition --
(Whole-Numbers-based, unit-interval Formal-Certainty Logic System)^(3^1)......
=
(Whole-Numbers-based, unit-interval Formal-Certainty Logic System)..+..
(Whole-Numbers-based, unit-intervals Ontological Possibility Logic System)..+.
(Whole-Numbers-based, unit-intervals Ontological Actualization Logic System)
-- and they abbreviate/assign ['(---)'] the two "ideo-ontologically" new terms/axioms-systems symbols thus generated essentially as follows --
Wq/EE_......(---)......WQ_
-- whose space is --
WQ...=...{q/0, q/1, q/2, q/3, . . . }
-- and --
Wq/EEE_......(---)......Wq/QE_
-- whose space is --
Wq/QE...=...
{b./0, b1(t)b./1, b2(t)b./2, b3(t)b./3, ...}.
The '.' "subscript" signifies unit-interval-restricted, "quasi-quantifiablility" of the qualifier "meta-numeral" so "subscripted".
The F.E.D. solution, or "semantification", for the second equation's second and third terms is based upon the following overall intuition --
(Whole-Numbers, Pure, Unqualified Quantifiers Arithmetic System)^(3^1)......=
(Whole-Numbers, Pure, Unqualified Quantifiers Arithmetic System)..+..
(Whole-Numbers-based, Pure, Unquantifiable Qualifiers Arithmetic System)..+.
(Whole-Numbers-based, Quantifiable Qualifiers Arithmetic System)
-- and they abbreviate/assign ['(---)'] the two "ideo-ontologically" new terms/axioms-systems symbols thus generated essentially as follows --
q/WW_......(---)......WQ_
-- whose space is --
WQ...=...{q/0, q/1, q/2, q/3, . . . }
-- and --
q/WWW_......(---)......Wq/QW_......(---)......WU_
-- whose space is --
WU_...=...
{uo/0, u1(t)uo/1, u2(t)uo/2, u3(t)uo/3, . . . }.
The 'o' "subscript" signifies "full-multiplicity quantifiablility" of the qualifier "meta-numeral" so "subscripted" [reflecting the "syncopated" notation for the generic <<Monad>>, or generic "qualitative unit", in Diophantus of Alexandria's circa 250 C.E. proto-ideographic-algebraical manuscript, The <<Arithmetike'>>].
Note that the second axioms-system -- the "contra-system" -- in each of the two progressions per the above "semantification"/solution is the same: the WQ_ axioms-system of arithmetic.
This implies that the WQ_ axioms-system is both a system of "dialectical ARITHMETIC" and a system of "[arithmetic for an algebra of] dialectical LOGIC".
Note that these two solutions, which converge and intersect in the WQ_ system for their second terms, diverge again thereafter, for the third terms of each.
The third system, or "uni-system", in each case, is qualitatively different from -- qualitatively unequal to -- the third system of the other case --
Wq/QE_......is qualitatively, "ideo-ontologically" unequal to......WU_.
For example, the bn(t) "quasi-quantifiers" of the Wq/QE_ system's "ontological qualifier" ontological category symbols, b./n, are restricted to the "Boolean" unit-interval. That is, they are "formal-logical quantifiers" -- "all (1), or none (0)" quasi-quantifiers -- whose only admissible values are confined to the "Boolean", "unit-interval end-points" set WE...=...{0, 1}, inherited from the WE_ component of this third, "uni-system" axioms-system as a "complex unity". The b./n "quasi-quantifiable ontological qualifiers" still connote whole ontological categories.
If, in a given dialectical progression being modeled using the Wq/QE_ system, the ontological category assigned to the ontological qualifier b./k actualizes during stage t, then the "quasi-quantifier" function for that qualifier, bk(t), in a well-fitting "meta-model", should generate the value 1 for stage t, so that the combined value of bk(t) and/"times" b./k will be 1b./k, or, equivalently, just b./k, indicating that the ontology assigned to category b./k is extant/manifest in stage t.
If, in a given dialectical progression being modeled using the Wq/QE_ system, the ontological category assigned to the ontological qualifier b./k does not actualize during stage t, then the "quasi-quantifier" function for that qualifier, bk(t), in a well-fitting "meta-model", should generate the value 0 for stage t, so that the combined value of bk(t) and/"times" b./k will be 0b./k, or, equivalently, just b./0, a "quanto-qualitative zero/absence" value, indicating that the ontology assigned to category b./k is unmanifest throughout stage t.
On the contrary, the un(t) full-multiplicity quantifiers [in the Whole-numbers sense] of the WU_ system's qualifiers, uo/n, range over the entire W space.
The uo/n "quantifiable qualifiers" do not make sense as connoting whole ontological categories, as do the q/n, and the b./n.
They do make sense as connoting the units, or <<monads>>, of the given ontological category, or <<arithmos>>.
If uo/k denotes a single unit, or <<monad>> of the ontological category, or <<arithmos>>, q/k, then the uk(t) "quantifier" function for that uo/k <<monad>>-ic qualifier, in a well-fitting "meta-model" of a given dialectical ontological progression, should generate the "population census count" -- the "number" of <<monads>> of kind, or, e.g., of <<genos>>, q/k -- that were/will-be extant as of stage t, e.g., the average number of type uo/k units / <<monads>> / logical-individuals that were/will-be in existence during epoch/stage t.
If uk(t)...=...0, then uk(t)uo/k...=...0uo/k...=...uo/0, which signifies either the extinction of all <<monads>> of the q/k <<arithmos>>, or the not-yet-manifest, not-yet-irrupted state of the q/k <<arithmos>>/ontology.
Thus, per the F.E.D. solution, the Wq/QE_ "uni-system" "inherits" the "unit-interval-endpoints" restrictedness that characterize its "quasi-quantifier functions", the bn(t), from its "<<arche'>>-system", the "Boolean" system of a formal-logic calculus, as simulated by an arithmetic restricted to the endpoints of the unit interval, i.e., restricted to 0 and 1, namely, the WE_ "<<arche'>>-system".
The WU_ "uni-system", on the contrary, "descends" from a "full-multiplicity" "<<arche'>>-system", the W_ system of "Whole numbers" arithmetic, and, consequently, shows that "inheritance" in its "full-W-multiplicity quantifier functions", the un(t).
The two dialectical systems-progressions considered in this post, per F.E.D., coincide neither in their first, "<<arche'>>-system", nor in their third, "uni-system", but only in their second, "contra-systems": wQ_ in both cases.
F.E.D. source materials for this post --
http://www.dialectics.info/dialectics/Briefs_files/_Brief1-29JUL2008_OCR.pdf
[pages 12 through 19 & pages 3-1 through 3-8].
http://www.dialectics.info/dialectics/Primer_files/3_F.E.D.%20Intro.%20Letter,%20Supplement%20A-1_OCR.pdf
http://www.dialectics.info/dialectics/Primer_files/3_F.E.D.%20Intro.%20Letter,%20Supplement%20A-1_OCR.pdf
[page A-42].
Regards,
Miguel
Regards,
Miguel