The F.E.D. "Meta-Boolean Proposition" -- The Fundamental "Law" of Dialectical Thought.

The F.E.D. "Meta-Boolean Proposition" -- The Fundamental "Law" of Dialectical Thought.



Dear Reader,

In 1854, George Boole published a ground-breaking treatise on the mathematics of logic entitled "An Investigation of the Laws of Thought", which sets forth an arithmetic, and an algebra for that arithmetic, which modeled classical Aristotelian logic, or "formal logic", and in which he arithmetically represented the class of all things, or the "Universe" class, for a given "universe of discourse", by the "Boolean" version of the number 1, and the class of no things, or "Nothing", by the "Boolean" version of the number 0.

Expressed in the language of that "Boolean algebra" of logic, Boole's "Fundamental Law of Thought" takes the form --

x(x).....=.....x

-- i.e., "x of x equals x", or "x squared equals x".


This "logic-equation" signifies that the self-reflexion of any category, denoted generically by the "unknown" value, x, simply reproduces that category itself, without any further "explicitization" of category x; without any change/development of that category whatsoever; without any "expanded reproduction" of that category e.g., a la Hegel's --

Being of Being.....=.....Being + Nothing


This 'logic-equation" also asserts either that "logical nonlinearity" does not exist, or, if it does exist, that it makes no difference -- that "logical nonlinearity" [e.g., x squared", i.e., x "to the power 2"] reduces immediately to "logical linearity" [e.g., to just x, i.e., to x "to the power 1"].

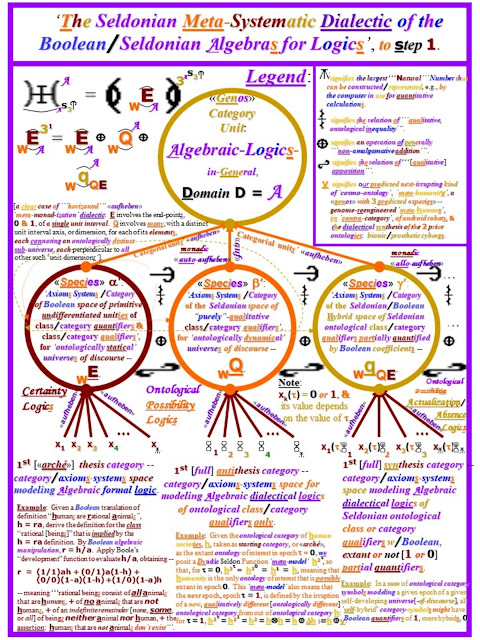
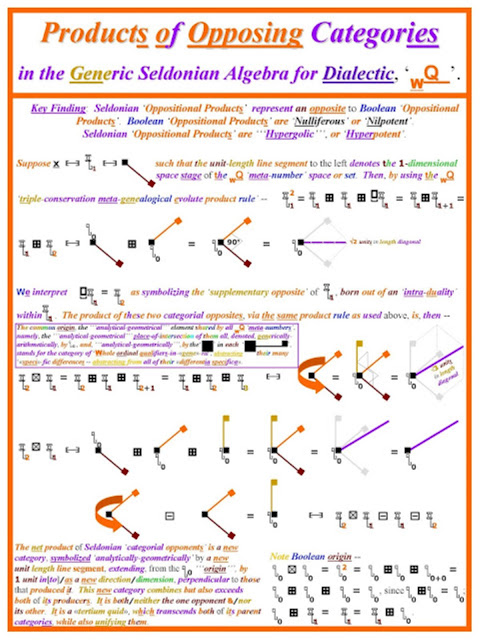
F.E.D. presents an immanent critique of the Boolean arithmetic for formal logic as one of the pathways to the discovery/evocation of their "First Dialectical Arithmetic", the "purely-qualitative" arithmetic of the NQ "meta-numbers", or "dialectors" --

NQ....=....{ q/1, q/2, q/3, . . . }.


Boole writes, in his "An Investigation of the Laws of Thought", that --

". . . we cannot conceive of the addition of any class x to the universe 1."

-- an assertion which, in its context, partially "explicitizes" the [partially] "Parmenidean" character that Boole presumed for all universes of discourse:  that all such universes must be ontologically statical rather than ontologically dynamical, never adding any new ontology to their content as a result of any immanent self-processing of their "old" ontology, by their "old" ontology, that they might exhibit.



The F.E.D. 'Meta-Boolean Proposition' is then the following --

'''Actual "universes-of-discourse" -- be they experienced by humans as "purely physical/external-to-mind", as "purely-mental/internal-to-mind", or as a hybrid of the two -- are inherently ontologically dynamical.'''

'''Actual "universes-of-discourse" are continually adding new classes, new kinds, new ontology -- new physio-ontology, new ideo-ontology, and/or new hybrids of the two -- to themselves.'''

'''The actual "fundamental law of human thought" must therefore be of the form of, not --

x(x)....=....x

-- but of the form of --

x(x)....=....x..+..delta_x

-- wherein "delta_x" denotes the purely-qualitative, categorial increment representing possible newly-born ontology, produced by the self-reflexive action -- in thought, internal to a human mind, and/or in the actuality external to that mind -- of x upon itself.'''

'''The F.E.D. NQ "meta-numbers", together with their axioms, found an arithmetic which instantiates this corrected "fundamental law of [dialectical] thought.'''



Regards,

Miguel