Dear Readers,
I have reproduced the content of the new
F.E.D. Vignette, below, in the typography native to this blog.
For the official rendition, using the full regalia
Encyclopedia Dialectica symbols palette, see the Vignettes Page at the
www.dialectics.org website --
http://www.dialectics.org/dialectics/Welcome.html
http://www.dialectics.org/dialectics/Vignettes.html
http://www.dialectics.org/dialectics/Vignettes_files/Aoristos_Dyosphainthos,v.1.0,F.E.D._Vignette_13,William_of_Ockham%27s_Dialectic_of_Science,posted_24MAY2013.pdf
Happy perusing!!!
Regards,
Miguel
F.E.D.
Vignette #13 --
William of Ockham’s Dialectic of Science --
A
Dialectical Episode in Early Medieval Philosophy
by
Aoristos Dyosphainthos
Author’s Preface. The purpose of F.E.D. Vignette #13 is to present
an E.D. ‘Dialectical Model Equation’
for a systematic dialectical method of presentation of the Early Medieval Philosophy of Science
of William of Ockham.
This ‘Dialectical Model Equation’
also serves as a “worked”, “cook-book” example, and sample, of the application
of the NQ dialectical algebra
to help organize, and to compactly encode, systematic expositions for ‘‘‘synchronic snapshots’’’ of the structure/process
of the living self-sustenance of systems -- ‘physio-systems’, ‘ideo-systems’,
and hybrids
of the two, such as the system of Science -- that are presently in existence; expositions that
explicate and assess the present
content of such systems, without explicitly expositing their ‘“diachronic chronicles”’
-- neither explicitly reconstructing the prior, diachronic history that constituted that
content, nor explicitly ‘pre-constructing’ any presently-predicted
future, successor
system of such. [Note: the ordering Mythopoeia, Religion, Philosophy, Science, Psychohistory is, per
the E.D. first
Psychohistorical-Dialectical ‘Meta-Equation’,
that of Human Ideology/Knowledge ‘Meta-Evolution’. See http://www.dialectics.org/dialectics/Aoristoss_Blog/Entries/2012/5/19_The_F.E.D._Psychohistorical_Equations.html ].
A Note about the On-Line
Availability of Definitions of F.E.D. Key Technical Terms. Definitions
of Encyclopedia Dialectica technical terms, including of E.D. ‘neologia’, are available on-line via the following URLs --
-- by clicking on the links associated with each
such term, listed, in alphabetic order, on the web-pages linked-to above.
Definitions of the Encyclopedia Dialectica special terms
most fundamental to this vignette are linked-to below --
«arché»
«arithmos»
and «arithmoi»
«aufheben»
Diachronic vs. Synchronic
NQ dialectical arithmetic/algebra
Systematic or Synchronic Dialectics
-- and we plan to expand these definitions resources
as the Encyclopedia Dialectica Dictionary Project unfolds.
[Note:
‘‘‘Arithmetical Quantifiers’’’
vs. ‘Arithmetical Qualifiers’. In the phrase “3 apples”, we
term “3” the “arithmetical [“pure”-]quantifier”, and “apples”
the ‘‘‘ontological’’’ -- or kind of thing -- ‘‘‘qualifier’’’. In the phrase “3 pounds of apples”, we term “pounds” the ‘metrical[-unit] qualifier’
-- or ‘‘‘unit of measure qualifier’’’
-- quantified by
the 3, which, together, ‘quanto-qualify’ the ‘ontological qualifier’, “apples”.
A key use-value of the dialectical arithmetics is to provide
algorithmic, ideographical-symbolic systems for the various kinds of
‘arithmetical qualifiers’,
both with and without the co-presence of ‘‘‘arithmetical quantifiers’’’.].
I. Introduction to the Subject Systematic Dialectic within Medieval Occidental Philosophy. The
present F.E.D. vignette sets forth a dialectical-ideographical
model of William of Ockham’s circa 1323 C.E. philosophical theory / ‘ideo-taxonomy’ of the sciences.
Ockham lived circa 1290 to 1349 C.E. [Common Era].
This vignette contains this
example of dialectical-mathematical models in general, formulated using a specific dialectical-mathematical language -- that of the “purely-qualitative”, “purely connotative” mathematics of
the ‘algorithmic-heuristic algebra’ of the NQ ‘arithmetic of dialectics’, which is an axiomatized algebraic dialectical logic.
For further background on
the algorithmics and the axiomatics of its ideographical, or “symbolic” dialectical logic -- or ‘algebraic
logic
of dialectics’’ -- see the www.dialectics.org website’s Briefs Page as well
as section II. of this vignette.
The core of Ockham’s philosophical theory of the sciences is as follows.
Ockham gave to terms of
language that refer to ‘non-term’ “physical facts”, the descriptor [the term] “categorematic”.
Thus, the “term”, or word,
“rock” refers to that “external-to-mind reality”, and is therefore a “categorematic” term.
Ockham gave to terms of language that refer
to, e.g., “categorematic” terms, i.e., to other terms
of language itself, the descriptor [the term] “syncategorematic”.
Thus, the “terms”, or words,
“all”, “some”, “none”, and “not” are all examples of such “word-referring
words”, or “term-referring-terms”.
Ockham also labeled terms
that refer to things belonging to the reality outside of [the reality of] language, by the
phrase “terms of the first intention”.
He labeled terms that refer to terms
of the first intension by the phrase “terms of the second intention”.
In the most direct sense,
then, “syncategorematic” terms are “terms of the second
intention”.
However, Ockham
distinguishes mere “terms” of language, in the sense
of individual words, from those higher-level /- higher ‘qualo-fractal
scale’ language constructions [constructions that we of F.E.D. call ‘meta-terms’, or ‘meta-words’, each one made up out of
a [usually] heterogeneous
multiplicity of mere “terms”, of mere individual words] which are named “complete sentences”, or “well-formed propositions”.
Ockham does not “reduce” the latter ‘ideo-ontology’ to the former.
Thus, for Ockham, categorematic terms, in ‘sentence-ial’ combination with syncategorematic terms, in the form of well-formed sentences or propositions, and, thus, functioning together, refer to, and describe, more adequately, typically, the things belonging to the reality outside of human
language, than do single, isolated, “mere” terms, or single, isolated words, such as those terms/words which are named
“names”, or “nouns”.
The sentence/proposition -- “All natural objects are transitory.”
-- is thus first intentional. Note: this
sentence “contains” [combines] both categorematic terms, like “natural objects”, and also syncategorematic terms, like “All”.
The sentence/proposition -- “All second-order-formal-logic axiomatizations of “Natural
Numbers” arithmetic are
either formally inconsistent or formally incomplete.” -- is thus second intentional [at least!]. Note that this sentence “contains” no terms which refer to non-linguistic, “physical” objects, but only terms which refer to other terms, or to the names of ‘‘‘mental objects’’’/‘‘‘idea-objects’’’, to ‘meme-ic’ or ‘memetic’,
human-Phenomic, ‘psychohistorical materialities’.
On the basis of these
distinctions, Ockham divides the «Genos» of the “Sciences” into two «species», or ‘sub1-«Gene» --
«species» 1: «Scientia realis», encompassing the sciences of “real things” [i.e., of external-to-mind, physical
things].
For example, the science of biology would form a sub1-«species» of this «species».
This «species» is first intentional.
«species» 2: «Scientia rationalis», encompassing the sciences of ‘noetic-things’ [i.e., of internal-to-mind, ‘Phenomic’ things].
For example, mathematics would form a sub1-«species» of this «species».
This «species» is second intentional.
For further background on
Ockham’s theory, see W. L. Reese, Dictionary of Philosophy and Religion, Eastern
and Western Thought, Humanities Press [Atlantic Heights, NJ:
1980], pp. 627 ff.
The two passages from the
source cited above that are most relevant to this vignette are extracted below:
“...Ockham makes an important
distinction between categorematic and syncategorematic terms [A.D.: a distinction in logic which harks back at
least to the Stoics; cf. also the work of Ockham’s predecessor, William of
Sherwood, circa 1210 to 1270 C.E.].”
“Terms which refer to
reality are categorematic, while terms which refer to categorematic
terms are syncategorematic.”
“Most common nouns are categorematic,
while words such as “not,” “all,”, and “some” are syncategorematic.”
“...Terms that refer to [A.D.: external-to-language/-mind] things are called terms of
first intention.”
“Terms referring to terms of
first intention are called terms of second intention.”
“In one sense the
syncategorematic terms mentioned above are second intentional; but, as Ockham
wishes to use the distinction, categorematic terms and syncategorematic terms,
functioning together, refer to [A.D.: external-to-language/-mind] things. “All men are mortal” is thus first
intentional.”
“But when we use terms such
as “genus,” “species,” and “difference” we are using terms of second
intention.”
“Propositions utilizing such
terms refer not to the world [A.D.: i.e., to the physical world,
external to the human-language/-mind “world”] but to terms of first intention.”
“...On the basis of the
distinction just mentioned, Ockham divides the sciences into two types [A.D.: into two «species»].
“Scientia rationalis, or rational science, is
second intentional. Logic is a science
of this type.”
“Scientia realis is first intentional.
Physics is an example of a science of real [A.D.:
external-to-language/-mind] things.”
The same source gives,
elsewhere [p. 563], a useful excursion into
the ‘philosophical etymology’ of the term “syncategorematic”:
“From the Greek syn
(“together”) and categorema (“predicate”).”
“The derivation may refer to
those terms which go together with the predicates or [to] those terms which
hold the predicates together; and thus, [to] those terms which cannot be
[intelligibly] used by themselves but only in conjunction with other
terms: e.g., “all,” taken alone,
has no definite reference to anything, but “all men” has.
“ “All” is syncategorematic
and “men” is categorematic.”
“In addition to the
quantifiers “all,” “some,” and “none,” included among syncategorematic terms
are “not,” “if...then,” “either...or,” and “both...and.”
II. E.D. Standard Interpretations for the Initial Generic Ordinal Qualifiers of the NQ Arithmetic. Perhaps a bit surprisingly, upon first apprehension,
the first four, first-order-logic, Dedekind-Peano Postulates for the “Natural” Numbers focus on their ordinality, not on their cardinality, viz. --
1. 1 is a “Natural Number”.
2. The successor of any “Natural Number” is also a
“Natural Number”.
3. No two, distinct “Natural Numbers” have the
same successor.
4. 1 is not the successor of any
“Natural Number”, i.e., 1 has no ancestor within
the “Natural Numbers”.
These postulates thus
identify the essence of the “Natural Numbers”, explicitly,
in terms of [apparently purely-] quantitative ordinality.
In keeping with this focus on the ordinal, Seldon defines the system
of the NQ dialectical arithmetic -- the first ‘antithesis-system’, or ‘contra-system’, to the “Natural Numbers” as «arché»-system -- in terms of qualitative
ordinality.
The NQ, which he also calls the ‘meta-Natural meta-Numbers’, are,
in their simplest, least-interpreted essence, a consecutive sequence of
‘meta-numeral’ ideograms representing the successive qualities, not the quantities, of ordinality -- the quality of ‘first-ness’, followed by the quality of ‘second-ness’, followed by the quality of ‘third-ness’, and so on... --
satisfying the four first-order-logic ‘contra-Peanic’, ‘Qualo-Peanic’ axioms:
1q. The ordinal qualifier for the quality of ‘first-ness’ is an element of the ‘consecuum’ of generic ordinal qualifiers.
2q. The successor of any element of the ‘consecuum’ of generic ordinal qualifiers is also an element of same.
3q. Any two, distinct ordinal
qualifiers have qualitatively unequal successors.
4q. The ordinal qualifier for the quality of ‘first-ness’ is «arché»: not the successor of any element of its ‘consecuum’.
The symbols, or ‘meta-numerals’, that stand for the ‘meta-numbers’ of the NQ ‘archeonic consecuum’ are derived, syntactically, in a way which represents
the semantic ‘self-subsumption’, ‘self-subordination’, or ‘self-demotion’ [dialectical, self-«aufheben» self-negation] of the “Natural Numbers”.
That derivation is part of the positive
fruition of the dialectical, immanent self-critique of the “Natural Numbers”, which
divulges the NQ as the implicit, most extreme known opposite, “Non-Standard
Model” of the “Standard”, Peano “Natural Numbers”.
It involves the turning of the ‘generic ordinal quantifiers’ of the “Natural Numbers” into the ‘generic ordinal qualifiers’ of the NQ ‘meta-Natural meta-Numbers’.
The conceptual ‘self-subsumption’ of the quantitative
ordinality intended by the Dedekind-Peano Postulates surfaces the NQ as their hitherto hidden,
implicit ‘intra-dual’, based upon the generic quality
of ordinality, a ‘‘‘genericity’’’ which we represent by the ‘meta-numeralic’ ideogram ‘q’.
That ‘meta-numeral component’ represents ‘qualitative ordinality’, or ‘ordinal quality’, in general: just ‘q’, or, more fully expressed,
just qN.
To fully express, ‘meta-numeral-y’, or ideographically, the ‘consecuum’ of specific ordinal qualities, namely --
NQ =
{‘first-ness’; ‘second-ness’; ‘third-ness’, etc.}
-- we must add a second ‘meta-numeral component’, via ‘‘‘subordinating’’’ specific “Natural
Numbers”, as specific ‘ordinal quantifiers’, to the generic ordinal
qualifier
symbol ‘q’,
by ‘subscripting’ those specific “Natural Numbers” to a ‘script-level’
‘q’, ‘‘‘above’’’ them, yielding --
NQ =
{ q1, q2, q3, ... }
[in which each ‘meta-number’ is a minimal, «genos»/«species» «arithmos eidetikos»
in its own right],
vs.
N = { 1, 2, 3, ... }.
Note that this opposition of an arithmetical system of purely-quantitative ordinality, based upon the N, versus an arithmetical system of purely-qualitative ordinality, based on the NQ, is not a radical dualism, imagined as an absolute, irreconcilable diremption between an absolute quantitative and an absolute qualitative.
This opposition is, on the contrary, a dialectical antithesis-sum.
The N quantifiers are still there, as ‘specifiers’ -- still present -- in, or ‘‘‘under’’’,
the generic qs of the NQ qualifiers, though subsumed, subordinated, demoted -- demoted to being their mere subscripts or denominators: The N quantifiers are still “contained” in[side] [‘‘‘beneath’’’]
the NQ qualifiers.
That is, each NQ qualifier is an «aufheben» determinate negation / conservation / elevation-into-one-step-higher-generality of an individual N quantifier.
The joint «aufheben» elevation of the quantitative
ordinals «species» yields the «genos» ‘q’, of the qualitative ordinals.
For this first layer of
interpretation of these “purely-qualitative” NQ ‘meta-numbers’ -- which does not yet make explicit their universal
interpretability for the modeling of dialectical progressions -- this is all that they
represent: abstract
temporality; [abstract chronological]
order; generic ‘ordered-ness’; the consecutive succession
of ‘qualitative ordinality’; the ‘consecuum’ of order quality or of order qualities.
But even here, at this
minimally-interpreted stage of the construction of the NQ dialectical arithmetic, there is already a kind of
generic ‘connotative entailment’ at work.
True, it is but a shadow, and but a
‘pre-vestigial’ harbinger, of the richness of the kind of particularity of categorial followership that drives forward,
intuitively, the dialectical, purely-qualitative logic of the more concrete, more specific dialectical-algebraic interpretations thereof.
A case in point is exemplified in the very NQ algebraic
model Ockham’s
dialectic of Science constructed herein.
This generic ‘connotative entailment’ can be formulated as
follows: ‘second-ness’ follows -- and even
follows from --‘first-ness’; ‘third-ness’ follows [from] ‘second-ness’, and so on.
In the next section, the
construction, by iterated interpretations layering, of the Seldonian first dialectical arithmetic will advance from this
harbinger of ‘connotative entailment’ to the following, still generic, but at last also explicitly
dialectical, form of ‘connotative entailment’ ordinality: ‘ first full antithesis follows from the self-interaction of [«arché»-]thesis; first full synthesis follows from the mutual interaction of first full thesis and first full antithesis’, and
so on.
III. Dyadic Seldon Function Interpretation of the Initial Generic NQ Ontological Category Qualifiers.
The generic ‘dialectical model meta-equation’ form for the functions-family
of the Seldon Functions is that of a generic cumulum symbol [‘|-|-|’] on the LHS [Left-Hand
Side] of the ‘dialectical meta-equation’, equated to an RHS expression
representing ‘self-reflexive operation’ of an [«arché», ‘‘‘seed’’’, ‘‘‘cell-form’’’, or ‘ultimate ancestor’ ontological category symbol [represented, generically, by [‘q1’] -- indicating its
recurring ‘self-reflexion’ via a ‘meta-exponentiated’, monotonically
increasing whole-number-valued ‘‘‘independent variable’’’ [‘h’ ] -- on the RHS of the generic Seldon Function
equation, viz. [with
‘generic-ness’ connoted by the
“rectangular” motif of the
symbols-set]:
|-|-|h = |[ q1 ]|vh, for h in { 0, 1, 2, 3, . . . }, v in {2, 3}.
If v = 2, the Generic Seldon Function
above is said to belong to the Dyadic Seldon Function sub-family.
If v
= 3, the Generic Seldon Function
above is said to belong to the Triadic Seldon Function sub-family.
Our remarks herein are concentrated on the Dyadic Seldon Functions,
because the main ‘dialectical-mathematical meta-equations’, modeling the dialectical-systematic presentation of Ockham’s Theory of Science, exposited herein, are
of the v = 2 variety.
With
v = 2, and selecting that special generic
Dyadic Seldon Function
form that we reserve for a systematic dialectic -- for
the dialectical-systematic method of presentation,
the form of the ‘model meta-equation’ to be
constructed herein becomes, more specifically --
)-|-(s = () qa ()2s , for s in { 0, 1, 2, 3, . . . }.
-- wherein the symbol s, replacing the more generic symbol h, takes on ‘‘‘systematic’’’, ‘‘‘taxonomic’’’ connotations, representing
the well-ordered, successive steps of a systematic exposition, and wherein, in general, the “curvilinear”
motif of the entire symbols-set
used is to connote the systematic dialectic domain of ‘dialectical modeling’.
The Seldon
Functions bring with them a further, second layer of
interpretation of the NQ qualifiers,
{ q1, q2, q3, ... },
by which they are interpreted as qualifiers that stand for generic dialectical ontological
categories, e.g., for ‘‘‘thesis’’’ categories, or for full or partial ‘contra-thesis’ categories, or for full or partial ‘uni-thesis’ categories.
If we assign
[ ‘[----)’ ] the «arché»-thesis category, qa, to the generic NQ qualifier ‘meta-number’, q1, as signed by ‘qa [----)
q1’, and if we can discern that qa, and all of its successor-categories, and their cumula, as generated by
its successive, cumulative,
‘Seldon-functional self-operations’, connote «aufheben» operators, that is, dialectical negation operators,
then the Dyadic Seldon
Function is seen to
signify, under the axioms of the system of arithmetic of the NQ ‘meta-numbers’
[
http://www.dialectics.org/dialectics/Correspondence_files/Letter17-06JUN2009.pdf
], a ‘self-iterated’, cumulative recurrence of dialectical “negations of [the]
negations”.
With every [unit] increase in s, the Dyadic Seldon
Function ‘formulaic recipe’ calls for the dyadic self-operation
of the result of the previous dyadic self-operation,
i.e., for a negation of the
negation of the result of the previous negation of the negation.
Only for s = 0 -- only for the case in which no self-operation occurs -- is the
“result” a singleton [ideo-] ontological
category symbol,
the symbol for
the «arché»
[ideo-]ontological category
alone, instead of that “result” taking the form of a cumulum of [powers-of-]two [or more] such
symbols, i.e., a “non-amalgamative sum” [cf. Musès], or an «a-sumbletoi»
sum [cf. Plato], of ‘[ideo-]ontological
category’ symbols,
since 20 = 1,
and since qa1 = qa --
)-|-(0 = () qa ()20 = () qa ()1 =
() qa () = qa.
For example, if we take epoch s = 1, and
denote the «arché» ontological
category simply by a,
for syntactical convenience, then the Dyadic Seldon Function calls for the following, as
per the NQ
axioms, since 21 = 2 --
)-|-(1 = () a ()21 = () a ()2 = () a
() x () a
() =
a + b.
-- wherein
a [----) q1 connotes the «arché» category
or ‘‘‘thesis’’’,
and where
b [----) q2 connotes the first ‘contra-category’ or ‘‘‘antithesis’’’,
with ‘+’ standing for a generalized addition operation, that encompasses
the addition
of qualitatively distinct terms, and with ‘x’ standing for a generalized multiplication operation,
that encompasses the multiplication
operation specific
to the NQ
qualifiers.
If we take ‘() a
() x () a
()’ with () a
() connoting the category to be dialectically negated, and with ‘() a
()’ connoting the category doing that dialectically [self-]negating, with ‘() a
()’ as the dialectical, determinate ‘negation-sign’ specific to () a
() as the object of the so-indicated
dialectical,
determinate negation
operation, then we have ‘() a
() x () a
()’, as a whole, as connoting
the first dialectical negation, by the negation-operation () a
() of the self-same negation
operation, () a
(), that is also the operand
of the negation-operator () a
(), forming what Seldon calls an
ideographical
‘subject [() a
()]-verb[() a
()]-object[() a
()] identical’,
and yielding the
first dyad:
‘‘‘thesis + antithesis’’’, or
‘«arché» category + first contra-category’, viz. --
() a
() x () a
() = qa + qaa =
qa + qb = a + b
-- which, in terms of the generic, minimally-interpreted NQ arithmetic, is a dialectical interpretation of the generic --
|-|-|1 = |[ q1 ]|21 =
|[ q1 ]|2 =
|[ q1 ]| |x| |[ q1 ]|
=
|[ q1 |+| q1+1 ]| =
q1 |+| q2.
The second
iteration of this dialectical negation of the negation,
corresponding to the consecutively next value of s namely, s = 2, for
the NQ arithmetic interpreted for [psycho]historical dialectics, yields the following,
ontologically-expanded cumulum
of ontological categories
-- a ‘dyad of dyads’,
consisting of 4 consecutive ontological categories:
)-|-(2 = () a ()22 = () a ()4 = () () a ()2 ()2 =
() a + b
()2 =
() a + b
() x () a + b () =
a + b + c + d.
The additional 2 ontological category-symbols above are dialectically interpreted, per the E.D. standard, as follows:
c = third ontological
category,
first full uni-category;
d = fourth ontological
category,
second contra-category.
We will not here pursue this E.D. standard dialectical interpretation of the ontological categories generated by the
generic Dyadic Seldon
Function beyond t = 2, because the ‘‘‘solution’’’
-- or ‘semantification’
-- of the category-terms generated by the ‘dialectical-mathematical meta-model meta-equation’ constructed in this vignette
[whose terms are generated, initially, as algebraic unknowns, terms of unknown meaning], as presented herein, does not
extend beyond that second
‘self-iteration’
for that ‘meta-model’.
The ‘purely-qualitative calculations’ illustrated above
describe our expectations for this ‘meta-model’ in terms of generic characterizations of the successive, consecutive dialectical categories.
The next section addresses the heart of this ‘meta-model’ -- the specific meanings of the generic dialectical categories as applied to
the special case
of the systematic dialectic of the Early-Medieval Philosophy of Science of
William of Ockham.
To begin our model of Ockham’s dialectical taxonomy of this universe-of-discourse of
human ideas, we use the dialectical logic axiomatized in an earlier letter
available via the www.dialectics.org Correspondence
Page --
-- and we enact the ‘‘‘mental action’’’ / ‘‘‘mental
operation’’’ signified by the ideogram ‘(----]’. That is, we “interpret” or “assign” q1, the first of the generic ‘meta-Natural meta-Numbers’ of our NQ,‘unquantifiable Qualifier’ ‘dialectical ideography’, or ‘dialectical symbolic logic’ [‘dialectical-ideographic logic’], as
follows --
q1 (----] qr, or q1 (----] r
-- such that r (----) “reality”, the universe of “real things”, outside of human language, outside of the human mind.
Our ‘dialectical-ideographic model’ then
captures a sequential, systematically-ordered, ‘‘‘ordinal-ized’’’ presentation of Ockham’s theory of the sciences, using the
connotations of the series of ideographical “shorthand” symbols that it generates algorithmically.
It does so via r as the recurrently ‘self-operating
operator’, ‘self-operation’, ‘self-function’, ‘self-refluxive function’,
‘‘‘self-reflexive
function’’’, or recurrently self-applied, connotationally
specific, determinate dialectical,
«aufheben»-negation
operation at the heart of the ‘self-iteration’ formula --
)-|-(s = () r ()2s
-- wherein s, as the higher exponent of the exponent 2, counts the “steps” or “stages” of that
systematic presentation
of the ‘idea-ontology’, or ‘ideo-ontology’-- of the ‘ideo-taxonomy’
-- of the philosophical categories, and wherein )-|-(s denotes the ‘cumulum’
-- meaning the connotative and non-amalgamative, ‘‘‘qualitative sum’’’,
or ‘‘‘superposition’’’ -- of the categories presented / ‘acCumulated’ as of step s of this “shorthand” ‘‘‘systematic-dialectical’’’ ‘present-ation’.
Let us, then, unfold this model step-by-step, starting
with step s = 0, then moving on to step s = 1, and thence onward to step s = 2, and, finally, to step s = 3, a step which immanently extends
Ockham’s theory to a category
of The Sciences
that Ockham, as far as we know, did not envision.
Step 0. The 0th step of this ‘presentation-model’, i.e., for s = 0,
since
20 =
2+1/2+1 =
2+1 x 2-1 =
2+1-1 = 1,
yields
--
)-|-(0 = () r ()20 =
r1 = r
-- which simply reiterates the starting point -- the «arché» ‘ideo-taxonomic category’ -- of this ‘present-ation’.
¿Does this categorial-singleton of step 0 grow into a ‘categorial-cumulum’ in step 1?
Step 1. For step s = 1 of this ‘presentation-model’, since 21 = 2+1 = 2, we
have --
)-|-(1 = () r ()21 = r2 =
r() r () = r “of”
r =
r “squared”
-- which connotes the ‘self-reflexive
function’, or ‘self-operation’, of the dialectical [«aufheben»] operation
denoted by r.
Syntactically, per the axioms of the NQ ‘meta-numbers’, we have the following values as the
content of step 1:
)-|-(1 = () r ()21 = r2 =
qr2 = qr + qrr
[----)
q1 |+| q1+1 = q1 |+| q2.
Our challenge, for this step, is to
“solve for” the new category, qrr, that is, to determine the meaning, the connotation,
of that new ‘categorogram’, given the already known/assigned meaning, or connotation,
of the ‘categorogram’ r =
qr.
So, let us apply the general ‘‘‘canon of interpretation’’’ of
such dialectical categories to the specific case of this
example.
Per that ‘‘‘canon’’’, the «arché» ‘categorogram’, r, is to be
interpreted, as stipulated, as connoting an «arithmos» of «monads» -- an assemblage of units -- each one of which is a “fact”, a physical, empirical “reality”,
“outside of” language and of the human mind.
Also per that ‘‘‘canon’’’, a symbol like qrr connotes the new category/«arithmos» that results
from the self-«aufheben» of the qr category/«arithmos», and, quite often,
that results from the self-«aufheben» ‘meta-monadization’ of some of the «monads» of the qr category/«arithmos».
That is, each «monad» or unit of the qrr «arithmos» / category / assemblage of units should be a ‘meta-«monad»’, made up out of a
multiplicity -- made up out of a ‘sub-«arithmos»’ -- of the «monads» of the qr «arithmos» / category.
So, the units of the qrr assemblage should be, in
this specific
case, ‘meta-realities’, ‘realities of second degree’,
each one made up out of a heterogeneous multiplicity of ‘realities
of first
degree’.
Also, the category qrr should be another category -- other than and to the
physical/empirical
“realities” category; a ‘meta-category’ to, and a ‘contra-category’
of, the r category.
Moreover, the qrr symbol should point to a category that is already
known to us, that is part of our synchronic, present conceptualized experience of the totality of The Sciences, and to a
category that is ontologically different than, and that is richer in
determinations than -- that is “more determinate” than -- that is more “complex”
and more ‘thought-concrete’ than, the r category.
On the bases set forth above, we propose that our
solution -- our ‘semantification’ -- of the syntactic term qrr should be t, connoting the «arithmos»/category of terms
of human language:
qrr = qt = t [----)
q2.
We propose this solution, in part, because the terms
of human language, as units,
are meta-units
of the units
of empirical/physical
“reality”.
Each term
of human language refers to, and represents, a heterogeneous multiplicity of
similar physical
“facts”.
The term “apple” maps to a large,
heterogeneous multiplicity of similar, physical
apples.
The term “orange” maps to a large,
heterogeneous multiplicity of similar, physical
oranges.
That is, “terms”
are general relative
to physical “facts.
One “term” typically
stands for a large, although still finite, set of similar physical situations.
Each “term” is an «aufheben» ‘meta-«monad»’ of a large number of similar “fact”-«monads».
Our solution for qrr is that qrr connotes the «arithmos»/category which has terms
of human language as its «monads».
In an historical, diachronic
sense, r “of” r also connotes
the natural-historical result of the ‘self-reflexion’, of the
‘bending-back-upon-self’, of “reality”; of the turning
back, upon itself, of physical “reality”, to form physical objects -- new
parts of that physical
“reality” -- that are capable of conscious reflection
upon physical “realities”,
including upon themselves.
In that historical, diachronic
context, this would mean the immanent emergence, within pre-human[oid] Nature, from out of
pre-human[oid] Nature
-- as part of the dialectic,
or of the self-development,
of Nature
itself -- of “observing eyes”, and of “observing sensoria” in general; of observing and
thinking minds, as also “things” / objects / bodies within Nature -- i.e., the
emergence of natural ‘[ev]entities’ which produce languages, hence “terms”,
to name / communicate their observations / experiences among themselves, as a
crucial part of their “struggle for existence” -- of their struggle for
successful expanded human[oid]-social reproduction.
But this consideration does not belong to synchronic, systematic dialectics in
itself.
It only represents the diachronic implications -- the pointers to past history, and to future history -- that are implicit in synchronic dialectics, but which
do not, as such -- as
diachronic --
form an explicit
component of the explanatory apparatus of synchronic, systematic dialectics.
Marx’s treatises on the dialectical, immanent critique of the
capitalist, ideology-ridden science
of “political economy”, are works of synchronic, systematic dialectics.
But, in Marx’s view, systematic
dialectics
is not absolutely
dirempt from diachronic,
historical dialectics.
Marx discussed this interconnexion between systematic dialectics and historical dialectics, as it arises in his extension of previous
concepts of dialectics
-- an interconnexion
which is, e.g., inaccessible to the eternally systematic, Parmenidean
dialectics
of Plato’s immutable
«arithmos eidetikos» --
in a crucial methodological passage from the Grundrisse:
“...our [A.D.: systematic-dialectical] method indicates the points where historical investigation
must enter in, or where bourgeois economy as a merely historical form of the
production process points
beyond itself to earlier historical modes of production.”
“In order to develop the laws of bourgeois economy,
therefore, it is not
necessary to write the real history
of the relations of production.”
“But the correct observation and deduction of these
laws, as having themselves become
in history, always leads to primary equations -- like the
empirical numbers e.g. in natural science -- which point towards a past
lying behind
this system.”
“These indications [Andeutung], together with a correct
grasp of the present,
then also offer the key to the understanding of the past -- a work in its
own right which, it is hoped, we shall be able to undertake as well.”
“This correct view likewise leads at the same time to
points at which the suspension
[at which the «aufheben» -- A.D.] of the present form of production relations gives signs of its becoming -- foreshadowings of the future.”
“Just as, on one side the pre-bourgeois phases appear
as merely historical,
i.e. suspended
[i.e., ‘«aufheben»-ed’ -- A.D.] pre-suppositions, so do the contemporary conditions of
production likewise appear as engaged in suspending themselves [i.e., in ‘«aufheben»-ating themselves’ -- A.D.] and hence in positing the historic
presuppositions for a new state of society.”
[Karl Marx, Grundrisse: Foundations of the Critique of
Political Economy (Rough Draft), M. Nicolaus, transl.,
Penguin Books [Middlesex: 1973], pp. 460-461, italics
only emphasis by Marx; combinations
of italic, underlined, bold, and color emphasis have been added by A.D.].
Accepting this solution, our step s = 1 dialectical-model equation thus becomes [with ‘D’ for the systematic-dialectic context’s
‘curvilinear, ontological delta
operator’, signifying the addition of an increment of new ‘ideo-ontology’] --
)-|-(1 = () r ()21 = r2 = qr2 =
r + Dr = r + t
[----)
q1 |+| q2
-- and we have the meaning that, as of step 1, s = 1, our model,
)-|-(s = () r ()2s,
posits the possible
existence of two
philosophical categories -- (1) the category of physical “realities”,
‘‘‘plus’’’ [signed by ‘+’, for connotatively “interpreted”, or “assigned”, ‘ontological qualifiers’, in
the ‘curvilinear symbols motif’ context
of systematic dialectics], (2) its
‘first contra-category’, of ‘‘‘terms of language’’’, both together comprising (1) the «physis»-«monads», or ‘fact-units’, of the physical realities’
«arithmos aisthetos», or sensorially-perceived
“facts”-assemblage, superposed
with, and ‘‘‘named’’’
-- in a many-to-one relationship -- by (2) the ‘trans-Platonian’
«arithmos eidetikos»
of terms-units,
or of terms-«monads».
¿How does this two-dimensional
‘possibility-space’, or categorial ‘ideo-ontology cumulum’, expand in step 2?
Step 2. For step s = 2 of this
presentation-model, since 22 = 2 x 2 = 4, we have
--
)-|-(2 = () r ()22 = r4 = r2 x 2 =
() r2 ()2 = () r + t
()2
-- which connotes the ‘self-reflexive
function’, or ‘self-operation’, of the collective dialectical operation -- of the two-category, two-dimensional
categories-cumulum operation -- denoted by
() r + t
().
Syntactically, per the axioms of the NQ ‘meta-numbers’, we have the following values as the
content of step 2:
)-|-(1 = () r ()22 = () r + t
()2 =
() r + t
() x
() r + t () =
() r + t
() + D() r + t () =
() t x () r + t
() () [using
Miguel’s shortcut] =
qr + qrr + qtr + qtt =
r + t
+ qtr + qtt
[----)
q1 |+| q2 |+| q2+1 |+| q2+2 =
q1 |+| q2 |+|
q3 |+| q4.
Our challenge, for this step, is to
“solve for” the two
new categories, qtr and qtt, that appear for the first time in this step, that is,
to determine the meanings, the connotations, the definitions, of each of these
new ‘categorograms’, as ‘connotative entailments’ of the already solved / known
/ assigned meanings / connotations /definitions of the ‘categorograms’ r = qr and t = qrr.
So, let us apply the general ‘‘‘canon of interpretation’’’ of
such dialectical categories to the specific case of this
example.
Per that ‘‘‘canon’’’, the ‘categorogram’ qtr connotes a new ‘uni-category’/hybrid «arithmos» -- the synthesis category --
that results from the «aufheben»
of the qr category/«arithmos», by
the qt category/«arithmos».
This often means a category/«arithmos» each of whose «monads» is a hybrid of the «monads» of the qr category/«arithmos» with
the «monads»
of the qt category/«arithmos».
Also per that ‘‘‘canon’’’, a ‘categorogram’
like qtr might also
connote ‘‘‘conversion’’’,
of «monads» of the qr category/«arithmos», into «monads» of the qt category/«arithmos».
Also, per that ‘‘‘canon’’’, the qtr symbol should
point to a category
that is already known to us, that is part of our synchronic, present conceptualized experience of the
totality of The Sciences,
and to a category that is ontologically different than, and that is richer in
determinations than -- that is “more determinate” than -- that is more “complex”
and more ‘thought-concrete’ than, all of the categories evoked in the preceding
steps.
And, per that ‘‘‘canon’’’, a symbol like qtt connotes the
new category/«arithmos» that results
from the self-«aufheben» of the qt category/«arithmos», and, quite
often, that results from the self-«aufheben» ‘meta-monadization’ of some of the «monads» of the qt category/«arithmos».
That is, each «monad», or unit, of the qtt «arithmos»/category should be a ‘meta-«monad»’, or ‘meta-unit’, of «monads» or units of the qt «arithmos» / category.
So, the units of the qtt assemblage should be, in
this specific
case, ‘meta-terms’, ‘terms of second degree’,
each one made up out of a heterogeneous multiplicity of ‘terms
of first
degree’.
Also, the category qtt should be another category -- other than all of the categories previously
evoked, in the preceding steps; a ‘contra-category’
of each of those categories, and a ‘meta-category’ / ‘meta-«arithmos»’ to the qt category / «arithmos».
Moreover, the qtt symbol should
point to a category
that is already known to us, that is part of our synchronic, present conceptualized experience of the
totality of The Sciences,
and to a category that is ontologically different than, and that is richer in
determinations than -- that is “more determinate” than -- that is more “complex”
and more ‘thought-concrete’ than, all of the categories evoked in the preceding
steps.
On the bases set forth above, we propose that our
solution -- our ‘semantification’ -- of the syntactic term qtr should be f, connoting the «arithmos»/category of Ockham’s propositions of the first intention:
qtr = qf = f [----) q3.
We propose further that our solution/‘semantification’
of the syntactic term qtt should be s, connoting the «arithmos» / category of Ockham’s propositions of the second intention:
qtt = qs = s [----)
q4.
In proposing these two ‘semantifications’, we are in
resonance with Ockham in invoking here, not
just a subdivision of the universe of terms of language, i.e., of
single words of language,
into two sub-universes, of “categorematic” words vs. of “syncategorematic” words, and
with “categorematic”
words
corresponding to qtr, and with “syncategorematic” words corresponding to qtt, so that qtr and qtt would fail to
differ, in terms of the ontology
of their «monads»,
from qt.
We hold that the ‘‘‘conversion’’’, i.e., the apt description, of
the «arithmos»/assemblage of physical “facts”, by “terms”, qtr, as of the «arithmos»/assemblage of “terms”, by “terms”, qtt, requires, in each case, something more than mere single words.
Human language is far more than the mere utterance of single word-sounds. Human language is, for starters, an «arithmos»/assemblage of sentences -- of propositions, that is,
of well-formed ‘meta-words’,
each one made up out of a heterogeneous multiplicity of words.
We thus hold that qtr must connote a
multiplicity of “terms” -- both “categorematic” and “syncategorematic”
alike -- combined, into well-formed sentences,
i.e., into propositions,
that describe our knowledge of the physical world, qr.
So:
qtr = qf = f [----) q3.
[cf. Boole’s
category of “Primary Propositions”, Laws of Thought,
Chapter IV, Proposition I.].
We thus hold also that qtt must connote a
multiplicity of “terms” -- both “categorematic” and “syncategorematic”
alike -- combined, into well-formed sentences,
i.e., into propositions,
that describe our knowledge of the secondary world of our own creation, of that core
component of ‘The Human Phenome’ which is the world of human language itself, qt.
So:
qtt = qs = s [----)
q4.
[cf. Boole’s “Secondary
Propositions”, Laws of Thought, Chapter IV, Proposition
I.].
Thus, f
connotes an «arithmos»/assemblage of “true” proposition-units,
or of proposition-«monads», that are about
-- of empirically-apt propositions which describe -- the physical world.
And, s
connotes an «arithmos»/assemblage of “true” proposition-units,
or of proposition-«monads», that are about
-- of cognitively-apt propositions which describe -- the world of human language, as an expression of the world of human thought.
But the assemblage of “true” propositions about the “real” world, external to
human thought, qtr, is what ‘‘‘the sciences of the real’’’
“contain”; is the ‘‘‘content’’’ of those sciences; is what Ockham means by ‘‘‘the sciences of the real’’’, by the
category he names «scientia
realis», which we will connote by l: f = l.
And the assemblage of “true” propositions about the “terms” world, the world
human language/thought, qtt, is what ‘‘‘the sciences of the rational’’’
“contain” for Ockham; is the ‘‘‘content’’’ of those sciences; is what Ockham
means by ‘‘‘the sciences of
the rational’’’, by the
category he names «scientia
rationalis», which we will connote by n: s = n.
Accepting these solutions, our step s = 2 dialectical-model equation thus becomes --
)-|-(1 = () r ()22 = r4 = () r + t
()2 =
() r + t
() x
() r + t () =
() r + t
() + D() r + t
() =
() t x () r + t
() () [using
Miguel’s shortcut] =
qr + qrr + qtr + qtt =
r + t
+ l + n
[----)
q1 |+| q2 |+|
q3 |+| q4.
-- and we have the meaning that, as of step 2, s = 2, our model,
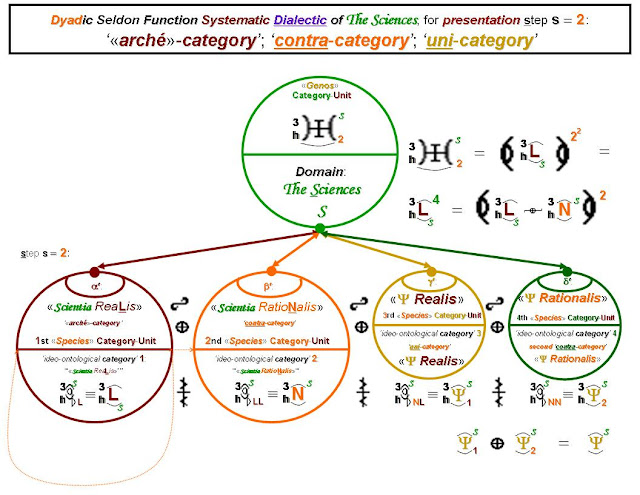
)-|-(s = () r ()2s,
posits the possible
existence of four
philosophical categories -- (1) the «arché» category of physical “realities”,
‘‘‘plus’’’; (2) its ‘first contra-category’,
of ‘‘‘terms of language’’’, ‘‘‘plus’’’; (3) the ‘first uni-category’
of the preceding two categories, whose units or «monads» are, as propositions, hybrids, combinations, or syntheses of
“categorematic” and “syncategorematic” terms, and, in
a sense, as “synthetic”
[cf. Kant] propositions,
hybrids of
the units of physical “reality’
with the units
of terms, thus constituting the category of propositions of the first intention, constituting Ockham’s «scientia realis», ‘‘‘plus’’’; (4) the ‘second contra-category’,
the category of propositions of the second intention, constituting Ockham’s «scientia rationalis», ‘meta-monadic’ with respect to
the «monads»
of the ‘first contra-category’,
of ‘‘‘terms of language’’’, given that these propositions, which are
the units or «monads» of the «scientia rationalis», constitute, each one, a ‘meta-term’,
or ‘term of the second degree’, each one made up out of a
heterogeneous multiplicity of ‘terms of the first degree’, which are
the units or «monads» of the category/«arithmos»/assemblage of units herein connoted by t.
All four
categories together, as an ‘ideo-cumulum’,
comprise --
(1) the «physis»-«monads», or ‘fact-units’, of the physical realities’
«arithmos aisthetos», or
sensorially-perceived “facts”-assemblage, superposed
with, and named -- in a many-to-one
relationship -- by;
(2) the
‘trans-Platonian’ «arithmos eidetikos»
of terms-units,
or of terms-«monads», both together superposed with;
(3) the
‘trans-Platonian’ «arithmos eidetikos»
of the propositions-units,
or of propositions-«monads», of the Ockhamian «scientia realis», all three together superposed with;
(4) the
‘trans-Platonian’ «arithmos eidetikos»
of the propositions-units,
or of propositions-«monads», of the Ockhamian «scientia rationalis».
¿But is there a next step, a step 3, for this classificatory, taxonomic, systematic-dialectic
presentation of
the Sciences?
Our step 2 models where this
dialectic
completed for Ockham, and for his times; for what was synchronic/extant in his
experience, and in the experience of his contemporaries.
Ockham saw, as far as we know, no other sub-categories
of Science
besides «scientia realis» & «scientia
rationalis».
¿But is there another sub-category of Science that was not synchronic/extant for Ockham, but that is synchronic for us?
¿How could this now four-dimensional ‘possibility-space’ of
categorial ‘ideo-ontology’ expand in a possible step 3?
Let’s see what arises if we iterate this model one
more step, i.e., for s = 3.
Step 3. For step s = 3 of this presentation-model, since 23 = 2 x 2 x 2 = 8, we have --
)-|-(3 = () r ()23 = r8 = r4 x 2 = () r4 ()2 =
() r + t
+ l + n ()2
-- which connotes the ‘self-reflexive
function’, or ‘self-operation’, of the collective dialectical operation -- of the four-category, four-dimensional
categories-cumulum operation -- denoted by
() r + t
+ l + n ().
Syntactically, per the axioms of the NQ ‘meta-numbers’, we have the following values as the
content of step 3:
)-|-(3 = () r ()23 = () r + t
+ l + n ()2 =
() r + t
+ l + n () x
() r + t + l + n () =
() r + t
+ l + n () + D() r + t
+ l + n () =
() n x () r + t
+ l + n () () [using Miguel’s shortcut] =
qr + qrr + qtr + qtt + qnr + qnt + qnl + qnn =
r + t
+ l + n + qnr + qnt + qnl + qnn
[----)
q1 |+| q2 |+|
q3 |+| q4 |+| q4+1 |+| q4+2 |+|
q4+3 |+| q4+4 =
q1 |+| q2 |+| q3 |+| q4 |+| q5 |+| q6 |+|
q7 |+| q8.
Our challenge, for this step, is to
“solve for” the four
new categories, qnr, qnt, qnl, and qnn,
that is, to determine the meanings, the connotations, the definitions, of each
of these new ‘categorograms’, as ‘connotative entailments’ of the already solved
/ known / assigned meanings or connotations of the ‘categorograms’ r = qr, t = qrr, l = qtr, and n = qtt.
Here, at this juncture, we wish to venture a
conjecture as to the ‘connotatively-entailed’ meaning-solutions, or
definition-solutions, of these four
new categories, qnr, qnt, qnl, and qnn.
In general, we see each of them as connoting
the fruition of the application
of the «scientia rationalis» -- i.e., of advanced formal, mathematical logic / dialectic -- to each
of the already-defined domains, resulting in their ‘‘‘subsumption’’’ by the «scientia rationalis».
We conjecture, more specifically, as follows --
- qnr =
the «scientia rationalis» ‘‘‘conversion’’’
of the «arithmos aisthetos» of physical facts; the rational-scientific
immanent critique, explanation [including theory of [past] perceptual error], and reconstruction of human perception
of the «realis» realm, extending to the formation of a universal, systematic-dialectical
taxonomy of
this realm, related to the project of the «Natur» division of Hegel’s Encyclopedia
of the Philosophical Sciences;
- qnt =
the «scientia rationalis» ‘‘‘conversion’’’
of the «arithmos eidetikos»
of terms of human language; the rational-scientific
immanent critique, explanation [including theory of [past] terminological error], and reconstruction of human language,
including the formation of a rational
universal language, comprising a dialectical phonetic language, or ‘dialectical phonogramy’,
as well as of a ‘dialectical pictogramy’,
and of a ‘dialectical ideogramy’,
related to Leibniz’s vision of a «characteristica universalis»; also related to the project
of the «Logik»
division of Hegel’s Encyclopedia of the Philosophical Sciences;
- qnl =
the «scientia rationalis» ‘‘‘conversion’’’
of the «arithmos»
of the propositions of the «scientia realis»; the rational-scientific immanent critique, explanation [including theory of [past] scientific theories error / ideology], and reconstruction of the «scientia realis», via the formation of ‘theories’ accounting for the differences in the history of different theories/ideologies,
or systems of propositions,
regarding the same “real” facts / physical phenomena, e.g.,
of different theories/ideologies of the same facts arising from different historical
epochs/human-social formations, related to the project of the «Natur» division of
Hegel’s Encyclopedia of the Philosophical Sciences, and to
that of Marx’s Grundrisse, A Contribution to the Critique of Political
Economy, and Capital: A Critique of Political Economy.
- qnn =
the «scientia rationalis» ‘‘‘conversion’’’
of the «arithmos»
of the propositions
of the «scientia rationalis» themselves; the rational-scientific immanent self-critique,
self-explanation
[including theory of [past]
scientific theories
error / ideology], and self-reconstruction
of the «scientia rationalis» by
the «scientia rationalis» themselves, including the formation of ‘meta-theories’
accounting for the differences
in the history of different
theories/ideologies, or systems of propositions, regarding the same mathematical and other “noetic” facts/phenomena, e.g., of different theories/ideologies of “the same” ‘‘‘noeta’’’ , or objects of thought, as they arise
in different historical epochs/human-social formations, extending to
development of a comprehensive mathematics
of dialectics
itself; related to the project of Hegel’s Science
of Logic, and especially to its second volume.
Note that Marx’s A Contribution to the
Critique of Political Economy, and Capital: A Critique of Political Economy,
provide a specific
example, and, mostly implicitly, a generic paradigm, for a core component of qnl as
conjecturally defined above.
Nothing
like Marx’s works was extant in Ockham’s time, but those works are ‘synchronic’ for us, today.
In those works, Marx addresses “...the
evolution of the economic formation of society ... as a process of natural history”
[Marx, Preface to the First German Edition
of Capital], and,
thus, addresses the human species and its ‘Phenome’ as a natural object, as a “real” fact/object, a part of the
purview of «scientia realis».
The
subsidiary objects which Marx addresses in those two treatises -- values, commodities, monies, capitals, and their “law
of [surplus-]value” -- are tied to objects of physical “reality” -- packages of tea, bank notes, steam-powered looms,
etc. -- but they are not
simply physical objects.
They are also noetic objects, ‘meme[t]ic objects’, ‘‘‘mental
objects’’’, ‘‘‘ideal objects’’’, ‘cultural objects’; ‘psyche-ic objects’, parts of the human-social “intersubjectivity”; parts
of ‘The Human Phenome’ -- human, “social relations of production” [Marx].
Such ‘category-[idea[l]-]objects’, such ideas, such
memes, residing within ‘The Human Phenome’, the very «arithmos [eidetikos]» of meme «monads», are “material”
not only in the sense that they are germane,
that they are salient, for Science, but also in that,
being “intersubjective”
-- held mentally, and behaviorally, in common among human actors -- they are also objective.
Such is the paradigm that we call ‘psychohistorical materialism’, pioneered by Marx.
Note also that this conjectured solution models the
research programme actually pursued by our co-founder, Karl Seldon.
The universe of discourse of our model of the
Ockhamian dialectic of Science, as updated, for our time, above --
)-|-(3 = () r ()23 =
r + t
+ l + n + qnr + qnt + qnl + qnn
-- is that of ‘the
elements [ facts and words ], and the sub-divisions, of knowledge [science]’.
If we abbreviate this universe of discourse,
restricting it to just “The
Sciences”, leaving its elements [ facts and words ] implicit therein, instead of making
them explicit, as
before, then perhaps we can encompass the most essential content of this systematic dialectic, or ‘synchronic ideo-taxonomy’, by means of a Triadic Seldon Function
of only three terms --
)-|-(1 = () L ()31 =
L + N
+ Y
-- instead of the earlier eight algebraic terms, but one
whose third and final algebraic term, Y, we must now define.
For the terms of this new model, we make the following
assignments to, or interpretations of, the terms of the old --
1. L (----) l;
2. N (----) n;
3. Y (----) () qnr + qnt + qnl + qnn ().
The ‘cumulum’
-- the superposition -- of the conjectured definitions of the ideographical terms
qnr, qnt, qnl, and qnn,
taken together, amount to a definition of the knowledge-field which we name ‘[socio-politico-economico-]psYchohistory,
or ‘psYchohistorical dialectics’, for
short, and ‘Y’ is our standard symbol for that knowledge-field.
It is conjectured here as a ‘‘‘complex unity’’’, or dialectical synthesis, of N & L, of logico-mathematical-cognitive-psYcheological
science
& physical science, including human social science as part of the science of natural history in
Marx’s sense:
Y = qNL.
The fuller development of Y is the intended
target and focus of the work of Foundation Encyclopedia Dialectica.
We can illustrate this proposed abbreviation, ‘dialectical-pictogramically’,
as --
The connotations of this Y encompass the
connotative content of the earlier model’s algebraic terms qnr, and qnl, and also qnt, since L
, itself ‘proxying’ l
-- and as the operand of N,
‘proxying’ n, in the formation of Y -- implicitly
connotes / "contains" the elements r and t.
However, it can be well-argued that the ‘self-reflexive moment’ of the earlier
model’s s = 3 step -- namely, its final algebraic term, qnn -- is missing from, this “abbreviated” model,
which thus has a gaping ‘homeomorphic defect’ as a model of that earlier model.
To get back this crucial component of the
Seldonian concept of psychohistory, while still retaining
some of the second model’s succinctness, we can convert the Triadic Seldon Function model back into a Dyadic Seldon Function model, still using the same
«arché».
Then the new dyadic model’s s = 1 step gives us Ockham’s dialectic, and its s = 2 step gives the Seldonian ‘extention’, with
Y = Y1 + Y2,
viz. --
V. Solution-Implicit Issue: ¿Did Ockham Intentionally Construct a DIALECTIC of Science?
Ockham was certainly no
stranger to concepts of “the dialectic”.
In the first place, medieval scholarship was permeated
by notions of, and discourses upon, dialectic, to an
extent which has yet to be fully explored and appreciated by modern scholarship.
In the introduction to her book Dialectic and
Its Place in the Development of Medieval Logic, Eleonore Stump
wrote:
“Since 1975 my
work in medieval logic has concentrated on dialectic.”
“I have tried to
trace scholastic treatments of dialectic to discussions of it in the work of
Aristotle, the Greek commentators on Aristotle, and the Latin rhetorical
tradition. But I have been especially
interested Boethius [F.E.D.: 480-525 C.E.], whose discussions of dialectic were among the most
important influences on scholastic treatments of the subject.”
“Accounts of
dialectic based ultimately on Boethius’s views continued to play a fundamental
role in philosophy through the fourteenth century.”
“The earliest
scholastic logician whose work we know, Garlandus Compotista [F.E.D.: Dialectica, circa
1054 C.E.], devoted a
great deal of attention to Boethian dialectic, and I have tried to follow the
development of scholastic dialectic from Garlandus through various
twelfth-century logicians (including Abelard) and thirteenth century terminists
into the fourteenth century... .”
“The scholastic
literature on dialectic is a vast treasure for scholarship, which even now is
largely unmined ... .”
[Eleonore Stump, Dialectic
and Its Place in the Development of Medieval Logic, Cornell University Press [Ithaca: 1989], p. 1].
In the second place, Ockham himself was a major
fourteenth century innovative contributor to medieval scholastic dialectic, principally via his circa
1323 treatise Summa
logicae, or “Summa[ry]
of All Logic”, including to the logic of “obligations”*.
Some of his innovative contributions were reviewed by Eleonore Stump in
the following terms --
“... there are
also contexts (notably that of dialectical disputation, discussed in
obligations treatises) in which types of inferences or rules for inferences
that would otherwise be perfectly acceptable produce paradoxical results.”
“...for instance, Ockham discussed cases in which the
otherwise acceptable rule ‘From the impossible anything follows’ does not hold.”
“In the
burgeoning study of consequences and the growing interest in obligations the
rather narrow formalization of logic brought
about by the terminists was stretched and
broadened. Ockham included a discussion
of obligations within his treatment of inferences, and he also considered a
broad variety of dialectical inferences.”
“In fact, he
blurred the boundary between dialectic and demonstration, thereby elevating
dialectic above the second-class status accorded it by the terminists.”
-- And --
“...contrary to the views of some contemporary
scholars, there is nothing in Ockham’s criteria for valid inferences which
corresponds to the notion of material implication in contemporary analytic
philosophy.”
“... syllogisms,
Topics, obligations, and insolubles are woven together in Ockham’s work into
one general account of inferences which is at once richer and broader than that
of the thirteenth-century terminists.”
“The terminists
tend to force all nonsyllogistic arguments, including dialectical arguments,
into syllogistic form. By contrast,
Ockham’s account of inferences recognizes a variety of nonsyllogistic
inferences, including dialectical and obligational inferences, without trying
to mold them into syllogistic form; and it includes syllogisms as one species
of consequences among others. The
result, which clearly represents an advance, is a development toward a logic
which is both formal and able to account for many sorts of inferences.” [Eleonore Stump, ibid., pp.
3; 8-9].
*[We have an
‘‘‘obligation’’’ here to define “obligation” as a term of logic. A respondent in
a formal disputation is said to hold an obligation to avoid
being forced into formally contradictory [“impossible”] assertions due to respondent
logical error, given that the original assertion upheld by the respondent
is a “possible” one.].
However, Ockham’s work on dialectics
was informed primarily by the dialectics of
Aristotle, specifically that of Aristotle’s Topics and Rhetoric,
and thus only indirectly, not directly, by the dialectics
of Plato.
We therefore cannot infer, with any certainty, that
Ockham consciously intended his ‘ideo-taxonomy’ of the Sciences to be anything
like a Platonian «arithmos eidetikos», especially
given Ockham’s “nominalist” views, rejecting Platonian and other hypostatizations
or reifications of “universals”.
More likely, Ockham’s ‘ideo-«genos»’ of the Sciences, and its two
‘ideo-«species»’
of «scientia realis» and « scientia
rationalis », were conceived within the prevailing Aristotelian «genus»/«species»
‘ideo-taxonomical’ tradition, which, though distantly related to Plato’s «arithmoi eidetikoi» dialectic,
represents a very attenuated form thereof, in the aftermath of Aristotle’s
critique and critical rejection of Plato’s «arithmoi eidetikoi».
Links to definitions of additional Encyclopedia Dialectica special
terms deployed in the discourse above --
«arithmos aisthetos»
«arithmos eidetikos»
categorial
category
‘cumulum’
dialectical categorial
progression presentations
homeomorphic defect
[The] Human Phenome
immanent
immanent critique
«monad»
ontological category
ontology
psychohistory
psychohistorical dialectics
qualo-fractal
qualo-Peanic
Seldon
Functions
‘self-meta-monad-ization’ or ‘self-meta-individual-ization’
or ‘self-meta-holon-ization’
