This blog tracks the ongoing new advances in Marxian Dialectics and regarding the Dialectic of Nature achieved by Foundation Encyclopedia Dialectica [F.E.D.], whose main website URL is www.dialectics.info .
Tuesday, July 29, 2014
Glossary Increment: The Generic, Dyadic-Dialectical [Self-]Movement of the [Self-]Expansion of Universe[-of-discourse] Ontology.
Dear Readers,
FYI: A new definitional increment is today being added to the www.dialectics.org website, Glossary Page -- defining the generic, dyadic-dialectical [self-]movement of the [self-]expansion of universe[-of-discourse] ontology.
For your convenience, I have also posted the JPEG image of that definitional increment here, below.
Regards,
Miguel
Sunday, July 27, 2014
Crafting Systematic-Dialectical, Categorial-Progression Presentations of [Sub-]Totalities -- The Principle of Sequential, Non-Redundant, Supplementary, ‘Determinate Oppositions’, and their Formulation via the Dyadic Seldon Function.
Dear Reader,
¡This blog-entry describes, for the
first time -- in a general, algorithmic manner -- the F.E.D.
method for
crafting systematic-dialectical, categorial-progression methods of presentation, starting
with the ‘dialectical-algorithmic’
generation of tables of contents, for dialectical-scientific theorizations of a vast
range of the various [sub-]totalities of human experience!
We have already,
‘repletely’ illustrated and instantiated this dialectical method
earlier in this blog, e.g. --
We have also
illustrated how the tables of content
of major dialectical expositions -- e.g., by Hegel, and by Marx --
embody these principles of exposition to a high degree, even though uninformed, at the times of their
craftings, by any explicitly algebraic, ideogramic-algorithmic guidance, although, as we
have shown, an intuitive, heuristic algorithm for dialectics was applied by both Hegel and
Marx -- two very different, but related, ‘dialectical heuristics’ in their two cases, both of which are
captured, generically, in the NQ_ axioms.
This time, for
this blog-entry, the general ‘dialectical algorithm’ of this dialectical method is the direct object of exposition.
But the exposition
of this abstract object will not
be richly meaningful except for those who already know, and/or who review, the
more concrete instantiations of this method, linked-to above.
I hope you will
enjoy these ‘heuristic-algorithmic’
insights into the crafting of dialectical
methods of presentation
specific to the ontological content of individual sub-totalities, and,
moreover, that you will find use-value in using this ‘dialectical algorithmics’ heuristic in the crafting
of systematic ‘‘‘tables of content’’’
for your own systematic-dialectical expository narratives.
Regards,
Miguel
We will play this
out four steps -- steps 0,
1, 2, and 3. Steps beyond step 3 are
analogous to step 3.
First: *Choose your starting category, or «arché», a,
as the simplest, most abstract category capturing the whole of the “organic
system” that you want to present, in systematic order -- simplest category to
most complex; most abstract category to most ‘thought-concrete’ --
a20 = a1 = a.
a20 = a1 = a.
Some Notes: ~a signifies the ‘self-determinate
negation/opposite’ of a, i.e., signifies aa
= a2. It does not signify the abstract nothingness, undialectical “negation” of a.
The expression x ~ y means that category x and category y are dialectical, determinate opposites of one another in terms of key determinations, or characteristics, of the content that they, respectively, connote.
The expression x ~+~ y means that category x and category y are co-present -- “added together” -- non-amalgamatively, because x and y are qualitatively heterogeneous in terms of the content that they connote.
The expression x ~ y means that category x and category y are dialectical, determinate opposites of one another in terms of key determinations, or characteristics, of the content that they, respectively, connote.
The expression x ~+~ y means that category x and category y are co-present -- “added together” -- non-amalgamatively, because x and y are qualitatively heterogeneous in terms of the content that they connote.
Then: *Interact a with itself
-- let your mind’s ‘ideo-formation’ of a enact an a [immanent or self-]critique
of a’s own shortcomings as a full-detail exposition of the “organic system” that
you wish to present -- thereby evoking into your awareness a’s
immediate, ‘‘‘next consecutive’’’, supplementary opposite category and counter-example, or
‘‘‘counter-category’’’, b --
a21 = a2 = a x a = a(a) = ~(a) = a ~+~ qaa =
a ~+~ b = a + b = (a & b).
The form '(a & b)' symbolizes more explicitly that we are asserting, as of the end of step 1, that BOTH category a and its 'determinate contra-category', qaa or b, are true for -- are characteristic of -- the "organic system" / sub-totality that we are presenting.
a21 = a2 = a x a = a(a) = ~(a) = a ~+~ qaa =
a ~+~ b = a + b = (a & b).
The form '(a & b)' symbolizes more explicitly that we are asserting, as of the end of step 1, that BOTH category a and its 'determinate contra-category', qaa or b, are true for -- are characteristic of -- the "organic system" / sub-totality that we are presenting.
Category qaa or b
is ‘counter-a’ and also ‘‘‘supplement to a’’’
in terms of ‘explicitizing’
more of the content immanent and implicit in the “organic system” that you wish
to present systematically and explicitly.
Next: *Interact (a
~+~ b) with itself -- let your mind’s ‘ideo-formation’ of (a & b) critique (a & b)’s own shortcomings as a
full-detail exposition of the “organic system” that you wish to present --
thereby evoking into your awareness both (1) the category c,
representing the categorial combination / unity of a and b,
which opposes
their initially apparently absolute, radical mutual opposition, and (2) b’s
immediate, ‘‘‘next consecutive’’’, supplementary opposite category and counter-example, or
‘‘‘counter-category’’’, d --
a22 = a4 =
a22 = a4 =
(a2)2 = (a
~+~ b)2 = (a
~+~ b) x (a ~+~
b)
= ~(a ~+~ b) =
b(a ~+~ b) =
b x (a ~+~ b) =
a ~+~ qba + b ~+~ qbb =
b x (a ~+~ b) =
a ~+~ qba + b ~+~ qbb =
a
~+~ b ~+~ c ~+~ d.
Category c
synthesizes/reconciles categories b and a: c =
qba.
Category d
is ‘counter-b’: d =
qbb.
In summary, step 2 new category d
is ‘contra-b’, and step 2 new category c is
‘combo(b, a)’.
KEY: But d is also
‘contra’, in some of its key characteristics/determinations, to each and all of a,
b, and c before it,
not just to b
alone --
d ~ c, b, [&] a.
Again: *Interact (a
~+~ b ~+~ c ~+~ d) with
itself -- let your own mind’s ‘ideo-formation’ of (a
& b & c & d)
enact a[n immanent or self-]critique of
(a ~+~ b ~+~ c ~+~ d)’s own shortcomings as a full-detail comprehension of the “organic system” that you wish to present -- thereby evoking into your awareness:
(1) category e = qda, representing the categorial combination / unity of a and d, which opposes their initially apparently radical mutual opposition, and;
(2) category f = qdb, representing the categorial combination / unity of b and d, which opposes their initially apparently radical mutual opposition, and;
(3) category g = qdc = qdba, representing the categorial combination / unity of d and c, i.e., of d, b and a -- i.e., of all previous opposites, d and b, with the «arché», a -- and which opposes their initially apparently absolute, radical mutual opposition, and;
(4) the final category of step 3, category h = qdd, which represents d’s immediate, ‘‘‘next consecutive’’’, supplementary opposite category and counter-example, or ‘‘‘counter-category’’’ --
(a ~+~ b ~+~ c ~+~ d)’s own shortcomings as a full-detail comprehension of the “organic system” that you wish to present -- thereby evoking into your awareness:
(1) category e = qda, representing the categorial combination / unity of a and d, which opposes their initially apparently radical mutual opposition, and;
(2) category f = qdb, representing the categorial combination / unity of b and d, which opposes their initially apparently radical mutual opposition, and;
(3) category g = qdc = qdba, representing the categorial combination / unity of d and c, i.e., of d, b and a -- i.e., of all previous opposites, d and b, with the «arché», a -- and which opposes their initially apparently absolute, radical mutual opposition, and;
(4) the final category of step 3, category h = qdd, which represents d’s immediate, ‘‘‘next consecutive’’’, supplementary opposite category and counter-example, or ‘‘‘counter-category’’’ --
a23 = a8
=
(a4)2 = (a
~+~ b ~+~ c ~+~ d)2 =
(a ~+~ b ~+~ c ~+~ d) x (a ~+~ b ~+~ c ~+~ d) =
~(a ~+~ b ~+~ c ~+~ d) =
d(a ~+~ b ~+~ c ~+~ d) =
d x (a ~+~ b ~+~ c ~+~ d) =
d x (a ~+~ b ~+~ c ~+~ d) =
a ~+~ qda + b ~+~ qdb + c ~+~
qdc + d ~+~ qdd =
a ~+~ b ~+~ c ~+~ d ~+~ e ~+~ f ~+~ g ~+~ h.
Category e
synthesizes/reconciles categories d and a: e =
qda.
Category f
synthesizes/reconciles categories d and b: f =
qdb.
Category g
synthesizes/reconciles categories d and c, i.e., categories d and qba:
g =
qdc = qdba.
Category h
is ‘counter-d’: h = qdd.
In summary, category h
is ‘contra-d’, category e is
‘combo(d, a)’,
category f is ‘combo(d, b)’, and category g is ‘combo(d, b, a)’.
category f is ‘combo(d, b)’, and category g is ‘combo(d, b, a)’.
KEY: But h is also ‘contra’, in
some of its key characteristics/determinations, to each and all of a,
b, c,
and d, the «arché» category, and the '"opposites"' categories that have been evoked before it, not just to d alone
--
h ~ g, f, e, d, c, b, [&] a.
We have a systematically ordered sequence of 'determinate oppositions' -- built from successive, progressive '''determinate negations''' -- additively combined with their 'determinate reconciliations'.
This 'Dyadic Seldon Function' dialectical method is a method of '''UNPACKING''', step-by-step, the '''dialectical contradictions''' -- the 'determinate oppositions', the 'intra-dualities', or, more generally, the 'intra-MULTI-alities' -- that, together with their [partial and full] dialectical resolutions, are internal to, and implicit within, the connotations of that '''historical [sub-]totality''', of that "organic system", of that domain.
A dialectical theorization and explanation of that organic system's, of that domain's, of that historical [sub-]totality's present, contemporary existence and mode of self-reproduction is thus being presented, synchronically and systematically.
That organic system's, that domain's, that historical [sub-]totality's inherent 'intra-MULTI-alities' are also immanent to -- implicit in the connotations of -- the beginning, the simplest, the most abstract, the «arché» category of, that '''historical [sub-]totality''' / "organic system" / domain.
We have a systematically ordered sequence of 'determinate oppositions' -- built from successive, progressive '''determinate negations''' -- additively combined with their 'determinate reconciliations'.
This 'Dyadic Seldon Function' dialectical method is a method of '''UNPACKING''', step-by-step, the '''dialectical contradictions''' -- the 'determinate oppositions', the 'intra-dualities', or, more generally, the 'intra-MULTI-alities' -- that, together with their [partial and full] dialectical resolutions, are internal to, and implicit within, the connotations of that '''historical [sub-]totality''', of that "organic system", of that domain.
A dialectical theorization and explanation of that organic system's, of that domain's, of that historical [sub-]totality's present, contemporary existence and mode of self-reproduction is thus being presented, synchronically and systematically.
That organic system's, that domain's, that historical [sub-]totality's inherent 'intra-MULTI-alities' are also immanent to -- implicit in the connotations of -- the beginning, the simplest, the most abstract, the «arché» category of, that '''historical [sub-]totality''' / "organic system" / domain.
Monday, July 21, 2014
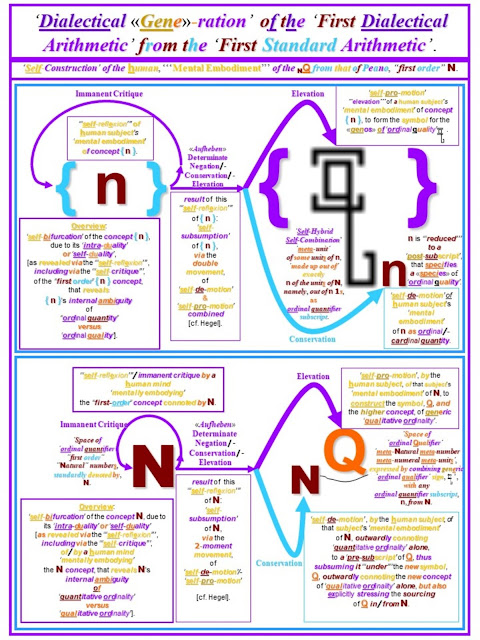
A '''Mind-Tool''' for Scientific Idealization, Self-Clarification, and Discovery.
Dear Reader,
The second
axioms-system in the Seldonian ‘‘‘meta-systematic’’’ method of presentation of
the progression of the axioms-systems of the Seldonian arithmetics / algebras
of dialectics, named NQ_, is the simplest, most
abstract, and least determinate -- in its expressive, descriptive capabilities
-- of all of the explicitly dialectical axioms-systems of
arithmetic / algebra in that systems-progression.
This does not mean, however, that the NQ_
system is the least useful
system in that progression.
It does not mean that one of the more
advanced dialectical-ideographic languages in that languages-progression is
always, in every case, to be preferred as the language in which to formulate
problems and in which to discover their solutions.
On the contrary,
the NQ_
system is perhaps the most
generally / universally useful of all of the systems in that
systems-progression -- and the most likely best place to start, for
‘heuristic-algorithmic’ support -- in the formulation of problems and the
search for their solutions.
¿Why?
¡Precisely because of its very
simplicity!
That abstractness
and simplicity gives NQ_ its methodological power, its power as a heuristic tool, because that abstractness
and simplicity facilitates scientific
idealization.
Most of the
details, complications, and potential distractions that threaten to derail a
more -- and a “too soon” -- determinate [but therefore also more “chaotic”, in the sense of Marx] description
of a problem, and not even expressible
in the language of the NQ_.
Descriptions of an
“external environment” of the central ‘‘‘eventities’’’ [beginning, of course,
with the ‘arché eventity’] to be dialectically modeled, and of that
environment’s interactions with / actions upon, those ‘‘‘eventities’’’;
descriptions of the physical spatiality of those ‘‘‘eventities’’’, and even of
their detailed
temporality -- all of these details must, at first, be stripped away, in an NQ_
formulation of a problem, or of a presentation.
All that remains,
after that “stripping away”, is a single, kind-of-being ‘arché category’, and the ‘meta-genealogy’ that proceeds out of it through the advancement of an abstracted -- minimal -- form of
temporality: ‘temporal ordinality’.
Regards,
Miguel
Subscribe to:
Comments (Atom)