‘Categories and «Arithmoi»’. -- Part 01: Seldon’s Secrets Series.

‘Categories and «Arithmoi»’.

-- Part 01: Seldon’s Secrets Series.

 

 

 

Dear Reader,

 

It is my pleasure, and my honor, as an elected member of the Foundation Encyclopedia Dialectica [F.E.D.] General Council, and as a voting member of F.E.D., to share, with you, from time to time, as they are approved for public release, by the F.E.D. General Council, key excerpts from the internal writings, and from the internal sayings, of our co-founder, Karl Seldon.

 

The first release in this new such series is posted below [Some E.D. standard edits have been applied, in the version presented below, by the editors of the F.E.D. Special Council for the Encyclopedia, to the direct transcript of our co-founder’s discourse].

 

In this 1st installment, Seldon describes his view of the relationship between dialectical, ontological categories, and the F.E.D.-resurrected, modern/ancient concept of «arithmoi».

 

Seldon --

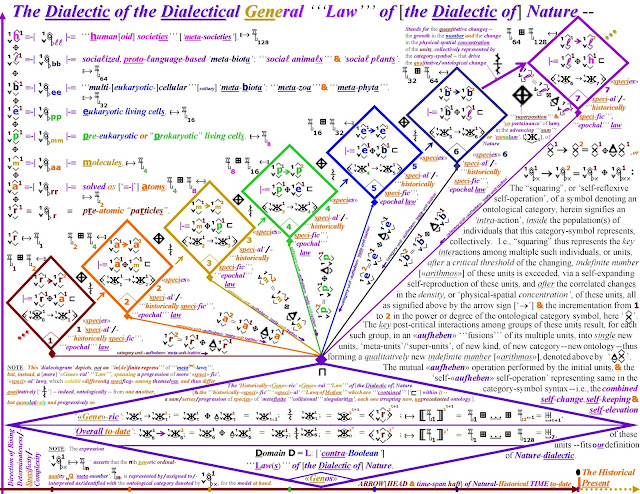
“Dialectic, in Hegel, and in Marx -- and even in Kant, Fichte, and Schelling – is about ontological categories and about ontological categorial progressions, categorial lineages, categorial combinations in, e.g., the form of categorial syntheses.  Dialectic is about progressions of categories involving inter-categorial oppositions, and their resolutions, and, more ‘subtlely’, is about intra-categorial oppositions.”

 

“An ontological category is a ‘single-ness’ that represents, that “stands for” a plurality:  the multiplicity of units or monads that all share the same quality that the singleness of the category comes to ‘mentally embody’, ‘uni-fying’ that monadic many-ness.”

 

“Thus, such categories are ‘arithmosic’.”

 

“An “arithmos” is a [mental] manifold, an ensemble of individuals, a ‘“number”’ of qualitative units.”

 

“Such an “arithmos” is also categorial if all of its units are not some random assortment, but if they all share [in] a common kind.”

 

“Plato, with his “arithmoi eidetikoi”, was really onto something -- despite the ‘eternalist’, ‘immutabilist’, ‘static-ist’, idealist shortcomings of his views.  His “eide”, his “ideas”, his “forms” – his ‘‘‘categories’’’, as they were later called, beginning, at least, with his pupil Aristotle, were also grasped by him as ‘arithmosic’, as ‘arithmoi’, as ‘‘‘numbers’’’ in that ancient, use-value mentality sense that the modern mentality, formed psychohistorically by the incessant practice of exchange-value exchange – of Marx’s “Elementary Form of Value” -- finds so difficult to reconstruct, to modernize, and hence to trans-modernize.”

 

 

 

 

For more information regarding these Seldonian insights, please see --

 

www.dialectics.info

 

 

 

 

 

For partially pictographical, ‘poster-ized’ visualizations of many of these Seldonian insights -- specimens of ‘dialectical art’ -- see:

https://www.etsy.com/shop/DialecticsMATH

 

 

 

 

¡ENJOY!

 

 

 

 

 

Regards,

 

 

Miguel Detonacciones,

 

Voting Member, Foundation Encyclopedia Dialectica [F.E.D.];

Elected Member, F.E.D. General Council;

Participant, F.E.D. Special Council for Public Liaison;

Officer, F.E.D. Office of Public Liaison.

 

 

 

 

Please post your comments on this blog-entry below!