The Goedelian Dialectic of the Standard Arithmetics

Dear Reader,

The plan to which I committed here, in an entry to this blog, on 17 September 2011 --

http://feddialectics-miguel.blogspot.com/2011/09/goedelian-dialectic.html

-- appended at the bottom of this blog entry, has now been fulfilled [although not entirely inside this blog]!

Or, rather, HALF-fulfilled!

A Part I. of II. of F.E.D. Vignette #4, a text entitled "The Goedelian Dialectic of the Standard Arithmetics" has just been posted to the www.dialectics.info web site --

http://www.dialectics.info/dialectics/Welcome.html

http://www.dialectics.info/dialectics/Vignettes.html

Link to Vignette #4

Part II. of II. is expected shortly.


As Karl Seldon himself -- the co-founder of F.E.D. -- has recently written, this text is the most comprehensive "how-to manual" yet published by F.E.D. on dialectical-mathematical modeling using the Seldonian NQ dialectical arithmetic/algebra.


This text explains in copious detail how to construct systematically-ordered dialectical, categorial progression presentations of general subject matter, which can be captured in four-symbol-element mnemonic expressions of the form --

a^(2^s)

-- [which take ~8 symbol-elements here, where we lack super-scripts, and super-scripts of super-scripts], exemplified by the expression --

N^(2^6)

-- which, through the repeated application of three axiomatic arithmetical rules, generates a 64-category explication of the "Natural" Numbers, "Whole" Numbers, "Integers", "Rational" Numbers, "Real" Numbers, "Complex" Numbers, and the first 'pre-vestige' of the "Hamilton Quaternions", and --

A^(2^4)

-- which generates a 16-category explication of the Value-Form Chapters of Marx's three-volume <<magnum opus>>, Capital: A Critique of Political Economy, including the Marxian categories of the Elementary Commodity Value-Form, the Expanded Commodity Value-Form, the General Commodity Value-Form, the Money Value-Form, the Money as Measure-of- Value Function category, the Money as Medium-of-Circulation Function category, the Money as Means-of-Payment Function category, the Capital Value-Form category, the Commodity-Capital category, the Money-Capital category, the Money-Capital-Mediated-and-Commodity-Capital-Mediated [Self-]Circulation of the Total Social Capital category, and the 'Self-Collision of the Capital-Value-System and the Transition Beyond It' category.

In particular, the first part of this new text provides a comprehensive background exposition whose coverages includes the following topics [note: an <<aporia>> [from ancient Greek] is a scientific impasse or quandary -- an apparently unsolvable problem] --

• The ‘‘‘Driver’’’ for the Progression of the “Standard Arithmetics”:   The Solution of “Unsolvable” Equations.

• The ‘Dyadic Seldon Function’ Equational ‘Meta-Model’ for the Progression of the “Standard Arithmetics”.

• Dialectic:  The Journey of the Progression of the «Aporia».

• ‘The Gödelian Dialectic’, or, “The Incompletability of Mathematics”.

• The Inherent, Ineluctable ‘Self-Problematicity’ of ‘Ideo-Formations’ [as of ‘Physio-Formations’].

• The Pedagogical Strategy Guiding System Order Choices for Our Presentational ‘Meta-Model’.

• The ‘Evolute-ness’ and ‘Cumulativity’ of Dialectical, Ontological-Categorial Progressions.

• Rules of Computation of the Dialectic Rules-System:  F.E.D.’s First Dialectical Arithmetic, NQ.

• Encyclopedia Dialectica’s ‘Organonic Algebraic Method’ for the Solution of Dialectical-Algebraic Equations.

• From ‘‘‘Formal Subsumption’’’ to ‘‘‘Real Subsumption’’’, and the ‘Culminant’/Epitome of the Latter.

Enjoy!!!



Regards,

Miguel




P. S. I am appending my earlier entry on this topic below, FYI --



"The Goedelian Dialectic of the Axioms-Systems of the "Standard Arithmetics" -- a Systems-Progression, 'Presentational Diachronic Meta-System', or "Meta-System-atic", Dialectic:


Dear Reader,

The F.E.D. "Dialectical Theory of Everything" theorizes, per F.E.D., not just the totality of the "external-to-human-mind", <<physis>>, "phys-io", "phys-ic-o", or "phys-ic-al" reality that humans experience, but also the totality of the "internal-to-mind" realm of "memes", of "idea-objects", or of <<eide>> that humans create and experience -- of '''the Human Phenome'''.

The latter, historically later realm includes human languages in general, including also "formal", "artificial", "ideogram-ic" languages, such as systems of arithmetic, represented by their axioms-systems, their <<arithmoi>> of axioms [their assemblages of axiom-units], i.e., of special sentences stating their rules.

Per F.E.D., the "historical material" of human history, includes not only what humans experience as "external-to-mind", physical material, but also the collective, inter-subjective "psycho-historical material" of this latter realm -- humanly experienced as "internal-to-human-minds" -- of language, of "memes", of idea-objects, of <<eide>> -- of the "human phenome".


F.E.D. holds that this latter realm has its own special "laws" of self-development, tied to the historical "self-meta-evolution" of the human social individual in terms of the "two [qualitatively] different sides" [Marx, Grundrisse] of the human-social individual, namely, the "side" of the human "social relations of production", and the "side" of the human "social forces of production".


F.E.D. also holds that these latter, later special "laws" of human-historical self-development constitute the "subject-matter" , the 'psychohistorical material', of the "meta-science" of "psychohistory", or of "psychohistorical dialectics".



Now, per F.E.D., a major discovery in the history of this "psychohistorical material-ism" [not explicitly presented as such by its discoveror] occurred circa 1933, in the pit of the last Global Great Depression, a discovery achieved by the logician, mathematician, and de facto physicist, Kurt Goedel.


Below, I paraphrase ['''] F.E.D.'s account of this, his discovery, with interspersed commentaries, and other textual variations, of my own.



'''You may never have heard of Kurt Goedel, a man who died in the mid 1970s.


However, the "news" about his extraordinary life story, and about his extraordinary accomplishments, is slowly leaking out to a wider world.

He is arguably the greatest logician since Aristotle, and the greatest mathematical logician of all time, to-date.

He was a close bud of Einstein's during their later years, when they were both contemporaneously honored by appointments to the prestigious Institute for Advanced Study, in Princeton, NJ.

Goedel even discovered a special solution to Einstein's Equations of General Relativity -- the first system of integro-differential equations to be capable of modeling the cosmos as a whole, at least from the point of view of the universal gravity field -- and a notoriously difficult-to-solve, or even, supposedly, "unsolvable in general", system of ten "simultaneous" NONLINEAR partial differential equations.

Goedel's celebrated special solution even predicted the possibility of a certain kind of time travel!

But the "physicality" of this solution is still in doubt, and it was but a backwater to the core of Goedel's scientific contributions.


From the times of Plato, Aristotle, and Euclid, circa 364 B.C.E., right up until the dissemination of Goedel's celebrated Incompleteness Proof, circa 1933 C.E. -- in the pit of the last Global Great Depression -- the consensus of academic philosophers, mathematicians, and scientists held that determining a set of -- supposedly "self-evident" -- fundamental sentences or propositions, called "postulates" and/or "axioms", and generating theorems from those premises by strict deductive logic, was the only secure way to true mathematical and scientific knowledge.

In 1930, Goedel proved, in his Ph.D. dissertation, his "Completeness Theorem" -- that the basic axiomatic deductive system of deductive logic itself -- called the "first order predicate calculus" -- was "complete" in the "semantic" sense -- in the sense of "meaning-content": essentially that the axioms of deductive logic were capable of supporting the deduction of every single sentence that is true or valid per our "intuitive" grasp of deductive logic.


Circa 1933, the world was learning of Goedel's second major, world-historical accomplishment -- his two "Incompleteness Theorems".

Goedel's Incompleteness Theorems prove that, within any deductive logical system able to deduce as little as "Natural" Arithmetic -- the arithmetic of the "counting numbers", {1, 2, 3, ... } -- or more, there must be a "well-formed" sentence of that system which can be shown, 'meta-deductively', to be, in fact, true, but which cannot be "decided" -- neither proved true, nor proved false -- by strict logical deductions from the axioms/postulates of that logico-arithmetical system, unless that system is "logically useless", i.e., is "inconsistent" -- meaning propositionally self-contradictory -- able to deduce both a proposition and its formal negation.

Goedel exploited, in proving his Incompleteness Theorems, a close analogue of the ancient paradox of Epimenides, which can be rendered, in essence, by the following sentence: "This sentence is false".

If you think through that Epimenides sentence, you will see that its truth-value appears to oscillate endlessly, back-and-forth, from True to False to True to False again, and again, and again, in your mind. . ..

Goedel's "undecidable" sentence essentially says of itself not that it is false, but that it is not a theorem of the logico-mathematical deductive system inside which it arises, i.e., that it is not logically deducible from the axioms/postulates of that logic/arithmetic system.

If such a sentence is true, then its logic/arithmetic system is incomplete -- unable to deduce all of its own, internally true propositions.

If such a sentence is false, then, even worse, its logic/arithmetic system is inconsistent -- able to deduce a false proposition.

So, Goedel thus proved that the method of rigorous logical deduction from axioms/postulates could never grasp "the whole truth" -- not even the "partial whole" of the truths contained within the logical system carved out by any given, limited set of axioms / postulates.

But Goedel's Incompleteness finding should not be taken -- as it typically is -- to be a static truth about any sufficiently-rich system of deductive logic/arithmetic.

As Goedel himself was repeatedly at pains to point out, his incompleteness findings locate the driver of a [potentially] infinite progression of cumulatively ever richer and more descriptively powerful logico-mathematical-scientific systems/languages, each successor such system «aufheben»-containing, but also «aufheben»-advancing beyond, and thus «aufheben»-superseding, its immediate predecessor system.

The process of this incompleteness-to-greater-partial-completeness movement of each such successor system/language of mathematics, as a "conservative extension" of its immediate predecessor mathematical system, thus negates, but also conserves, and also elevates, into a higher, more inclusive, system, its immediate predecessor system, thus meeting the definition of an «aufheben» process, that is, of a dialectical process.


That is, Goedel's Incompleteness Theorems logically predict a potentially infinite cumulative «aufheben»-progression of number sets / number systems / number spaces, and of axiomatic systems of arithmetic for those numbers and their spaces -- what Goedel called the "inexhaustibility" of mathematics.

Goedel thus discovered, via his Incompleteness Theorems, 'The Gödelian Dialectic', logically immanent in mathematics!

Goedel himself formulates this in terms of philosopher Bertrand Russell's "theory of logical types".


Let's say that a set that "contains" only the names of non-set idea-objects, "Ur-objects", like, say, that of the Earth and that of the Sun and that of the Moon, is of Russellian "logical type" 0, since it "contains" no braces.

Then a set which "contains", as its "deepest" object/member, the set { Sun, Moon } itself, i.e. --

{ Earth, Sun, Moon, { Sun, Moon } }

-- denotes, in "extensional" form, the "intension", or quality, that both the Sun and the Moon share in common, and is thus of logical type 1 [ since it "contains" 1 pair of braces -- "contains" 1 level of {...}-parenthetical enclosure-depth more or deeper than the minimal, 0-depth, outer-only parenthetical enclosure of set content, which defines logical type 0, as we described above].

A set containing, as its "deepest" object/member, the set-containing set {Earth, { Moon, Sun } }, e.g. --

{ Earth, Sun, Moon, { Sun, Moon }, { Earth, { Moon, Sun } } } --
-- denotes the quality that the Earth shares in common with the common quality shared by the Sun and the Moon, and is of logical type 2 [since it "contains" braces to depth 2 ], and so on.



Here is the formulation of 'The Goedelian Dialectic' in Goedel's own words --


"...For any formal system you can construct a proposition — in fact a proposition of the arithmetic of integers — which is certainly true if the system is free from contradiction but which cannot be proved [or disproved — F.E.D. ] in the given system" [the foregoing summarizes Goedel's "First Incompleteness Theorem" — F.E.D.].

"Now if the system under consideration (call it S) is based on the theory of types, it turns out that exactly the next higher [logical— F.E.D.] type not contained in S is necessary to prove this arithmetic proposition, i.e., this proposition becomes a provable theorem if you add to the system the next higher [logical— M.D.] type and the axioms concerning it." [Kurt Goedel, "The Present Situation of the Foundations of Mathematics (*1933o)", in S. Feferman, et al., editors, Kurt Goedel: Collected Works [Volume III: Unpublished Essays and Lectures], Oxford Univ. Press [NY: 1995], p. 46, emphases added by F.E.D.].



Again:

"If we imagine that the system Z [a formal, logical, propositional-/predicate-calculus system inclusive of "Natural" Numbers' Arithmetic, NOT the full system of the positive and negative Integers, and zero [zero being both[, or neither] positive and[ nor] negative — F.E.D.], standardly also denoted by Z — F.E.D.] is successively enlarged by the introduction of variables for classes of numbers [M.D.: thus of logical type 0, if individuals numbers are taken to be the non-set "Ur-objects"], classes of classes of numbers [M.D.: thus of logical type 1, if individuals numbers are taken to be the non-set "Ur-objects"], and so forth, together with the corresponding comprehension axioms, we obtain a sequence (continuable into the transfinite [per those who accept assertions about "actually infinite" constructions that, because infinite, cannot actually be performed by mathematicians — F.E.D.] ) of formal systems that satisfy the assumptions mentioned above, and it turns out that the consistency ... of any of these systems is provable in all subsequent systems."

"Also, the undecidable propositions constructed for the proof of Theorem 1 [Goedel's "First Incompleteness Theorem" — F.E.D.] become decidable by the adjunction of higher [logical— M.D.] types and the corresponding axioms; however, in the higher systems we can construct other undecidable propositions by the same procedure."

"...To be sure, all the propositions thus constructed are expressible in Z (hence are number-theoretic propositions); they are, however, not decidable in Z, but only in higher systems..." [Kurt Goedel, On Completeness and Consistency (1931a), in J. van Heijenoort, editor, Frege and Goedel: Two Fundamental Texts in Mathematical Logic, Harvard University Press [Cambridge: 1970], p. 108, emphases and [square-brackets-enclosed commentary] added by F.E.D.].



Now, here's there clincher --

For each, successive logico-arithmetical system in the Goedelian progression of such systems, Goedel's "undecidable" meta-mathematical proposition, denoted G -- neither provable nor disprovable from the premises of its logical system -- maps into the "object language" of that logical system of arithmetic+ inside which it arises, that is, it "deformalizes", to an "unsolvable" algebraic equation --

"... The Goedel sentence G... asserts its own undeducibility from the postulates...."

"Deformalizing G... we see that under the standard interpretation it expresses a fact of the form [for every n-ary list of number-components of x such that each number-component is a member of the set of 'diophantine', or "Natural", Numbers in use — F.E.D.] ...


[for every x in Z -- M.D.]

fx does not equal gx ...


[the expression to the left is just a generalized, generic expression of the kind of simple "unsolvable" algebraic equations that I plan to present in a subsequent posting to this thread, on "The Goedelian Dialectic of the Standard Arithmetics" — M.D.],

where f and g are n-ary polynomial[ function]s. ..."

"An [in]equation

[for every x from Z -- M.D.]
fx does not equal gx,

where f and g are two such polynomial[ function]s, is called diophantine [after Diophantus of Alexandria, a crucial figure in our story, as we shall see, who, circa 250 C.E., wrote the earliest known book on arithmetical proto-ideographic Algebra, entitled "The «Arithmetiké»" — F.E.D.] ...."

"By a solution of the equation we mean an n-tuple a of natural numbers such that

[there is at least one a from Z such that -- M.D.]
fa = ga... ."

"So G;... asserts the unsolvability of the...equation fx = gx, and the proof of [Goedel's "First Incompleteness Theorem" — F.E.D.] produces... a particular diophantine equation that is really unsolvable [unsolvable within the given axiomatic system of arithmetic, and also within all of its predecessor systems of arithmetic, but solvable within all subsequent systems of arithmetic, starting with the next/successor system of arithmetic, incorporating the next higher logical type, and the axioms governing that higher logical type, which corresponds to the next higher kind of number, as we shall see — M.D.], but whose unsolvability cannot be deduced from the postulates..." [Moshé Machover, Set Theory, Logic, and their Limitations, Cambridge University Press [Cambridge: 1996], pp. 268-269, emphases and [square-brackets-enclosed commentary] added by F.E.D.].

That is, the undecidable proposition into which Goedel's undecidable "I am not a theorem of this logical system of arithmetic" proposition "deformalizes" -- a true proposition, but one that is "undecidable" -- one that cannot be either proven or disproven within the axioms-system of arithmetic in which it arises -- a true proposition asserting that a certain algebraic equation cannot be solved [within the given logical system of arithmetic] -- not only becomes a decidable, deductively-provable proposition within the next higher[-in-logical-type] logical system of arithmetic, but the "unsolvable" equation of that proposition, and of that predecessor system, becomes a solvable equation in that same successor system, as well as in all of its successor systems, using the new kind of number that results from the successor system's incorporation of sets of the next higher logical type.

Goedel's Incompleteness Theorem is thus the theoretical prediction and explication of the -- in our terms -- psychohistorical dialectical -- or «aufheben» -- progression of the expansion of arithmetic, of the expansion of the kinds of number -- i.e., of the expansion of 'number idea-ontology' -- and of the conversion of "unsolvable" equations into SOLVED equations, that we will see by way of examples in my planned subsequent post here on The Goedelian Dialectic of the Standard Arithmetics.

The discovery of the zero "kind of number", of the "negative" "kind of number", of the "fractional" "kind of number", of the "irrational" "kind of number", and of the "imaginary" "kind of number", etc., are all behind us in history -- the legacy of our ancestors' solutions to their ancestors' "unsolvable" problems.


But, here and now, what is the next expansion of 'number idea-ontology', beyond the kind of number officially known today, that is needed to solve the "unsolvable" equations, and the related theoretical and practical, technological and general societal problems, of our own time?'''




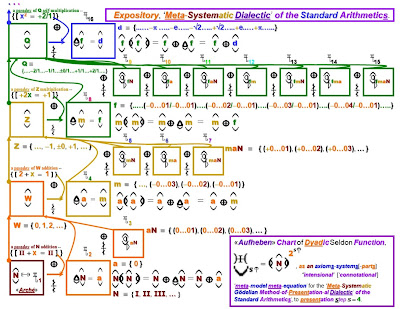
In a subsequent post to this thread, I plan to present my reconstruction of the F.E.D. equational dialectical "meta-model", of "The Goedelian Dialectic" of the Standard Arithmetics' Axioms-Systems, expressed via the algebra of the NQ "First Dialectical Arithmetic", and via a Dyadic Seldon Function, modeling the processes, and the contents, of this "Goedelian Dialectic", i.e., for [using spectral-ordinality textual color-coding: red-orange-yellow-green-blue-indigo-violet] --


N ---> W ---> Z ---> Q ---> R ---> C ---> H ---> . . .


--wherein --

N connotes the axioms-system of the arithmetic of the "Natural Numbers", N;

W connotes the axioms-system of the arithmetic of the "Whole Numbers", W;

Z connotes the axioms-system of the arithmetic of the "Integers", Z;

Q connotes the axioms-system of the arithmetic of the "Rational Numbers", Q;

R connotes the axioms-system of the arithmetic of the "Real Numbers", R;

C connotes the axioms-system of the arithmetic of the "Complex Numbers", C, and;

H connotes the axioms-system of the arithmetic of the Hamilton "Quaternions", H, . . ."