The Goedelian Dialectic and Knowledge Representation Condensation

Full Title: The Goedelian Dialectic, Knowledge Representation Condensation, and The Dialectical Operations Stage of Human Adult Cognitive Development.


Dear Reader,

Part II. of II. of F.E.D. Vignette #4, "The Goedelian Dialectic of the Standard Arithmetics", was just posted to the www.dialectics.info website.

The scope and content of Part II. is rather replete, but, for the purposes of this post, I want to quote its discussion of just one topic, that shows how accession to the dialectical operations stage of human adult cognitive development -- transcending the last Piagettian "formal operations" stage -- can open, among many other new vistas, new vistas of knowledge representation condensation.

Below I have reproduced Part II., pages II-58 through II-59, as best as the available typography here will allow.

The definitions of the symbols for the axioms-systems of arithmetic used in the extract below are as follows:

N# connotes the axioms-system of the arithmetic of the "Natural Numbers", N;

W# connotes the axioms-system of the arithmetic of the "Whole Numbers", W;

Z# connotes the axioms-system of the arithmetic of the "Integers" [in German, <<Zahlen>>], Z;

Q# connotes the axioms-system of the arithmetic of the "Rational, or Quotient, Numbers", Q;

R# connotes the axioms-system of the arithmetic of the "Real Numbers", R;

C# connotes the axioms-system of the arithmetic of the "Complex Numbers", C;

H# connotes the axioms-system of the arithmetic of the Hamilton "Quaternions", H;

O# connotes the axioms-system of the arithmetic of the Cayley/Graves "Octonions", O;

K# connotes the axioms-system of the arithmetic of the "William Kingdon Clifford Numbers", K;

G# connotes the axioms-system of the arithmetic of the Grassmann "Geometric Numbers", G, and;

X# connotes the axioms-system of the arithmetic of the [unknown] "next" arithmetic, X, . . .


"Symbolic Economy, Semantic Density / Semantic Productivity, and Mnemonic Power.

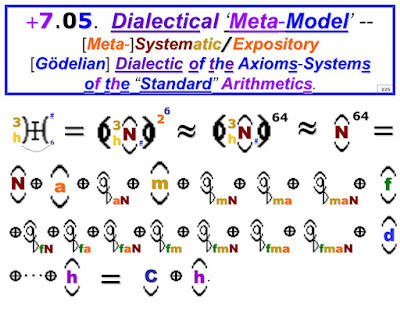
The ‘Dialectical Equation’ that constitutes our ‘meta-model’ of the systems of the ‘‘‘Standard Arithmetics’’’--

#)-|-(s.....=.....(.#N.)^(2^s)


-- functions also as our Encyclopedia Dialectica definition of ‘‘‘Standard Arithmetic’’’.


As such, it is a dialectically ‘‘‘open-ended’’’ kind of definition.


No final term, no ultimate ‘meta-meristem’, no closing ‘‘‘culminant’’’, is specified in this ‘meta-model’, by its ‘Dialectical Equation’.



It remains a ‘“potentially infinite”’ [cf. Aristotle] sequence of series, though one which is always, at any given moment of Terran human history, actually [meta-]finite in terms of that part of its infinite potential which has been actualized by Terran humanity so-far.

This ‘dialectical definition’ of ‘‘‘Standard Arithmetic’’’ is therefore not simply N#, or W#, or even C#, or H#, or O#.


It is, on the contrary, the entire ‘meta-system-atic’, dialectical and cognitive movement from N# to W#, from W# to Z#, from Z# to Q#, from Q# to R#, from R# to C#, from C# to H#, from H# to O#, and beyond, that is summarized by, and “contained in”, that ‘Dialectical Equation’ --

....N#...---)...W#...---)....Z#...---)....Q#...---)...R#...---)...C#...---)...H#...---)...O#...---)...K#...---)...G#...
s:.1......---).....2.......---).....3......---)......4......---)....5......---).....6......---)....7......---)....8......---).....9......---)..10 ...

-- both actually [e.g., to K# and to G#.], and potentially [to arithmetics beyond those that have been actualized -- codified or axiomatized -- by Terran humanity to-date], given the “incompletability or inexhaustibility” of mathematics in general, and of arithmetics in particular, established by Gödel.

However, confronted with the potential infinity of such encyclopedic dialectical-equational definitions, we must grapple with issues of the ease and compactness of their ‘representability’ via our 'dialectical arithmetics’, and via their ‘dialectical algebras’.


Doing so, we find that our situation is, indeed, quite favorable in that regard.


If we strip the ‘Dialectical Equation meta-model’ that forms the core of this essay down to its bare essentials, stripping off all of the helpful but inessential taxonomical locator epithets, or ‘dialectical diacritical marks’, then our most condensed concentration of the meaning of this entire essay requires just four symbols, or symbolic elements, namely, the elements ‘_’, ‘N’, ‘2’, and ‘6’, arrayed as follows --

N^(2^6)

-- such that the 4 symbolic-elements above [given font logistics supporting superscripts, and superscripts of superscripts], so arranged, can replace, e.g., the entire 64-term, ~641 symbolic-element expression that concludes the core section of this essay. They can do so in this sense: the entire 64-term series can be re-constituted and recovered, from the 4 symbol, ‘semantically concentrated’ version, simply by repeatedly applying 3 simple rules -- i.e., just 3 of the 9 core axioms of the NQ space of dialectical arithmetic, as given herein within section B.i. -- namely, Axioms §7, §8, and §9 --


§7. For all n in N:...qn + qn....=....qn.

§8. For all j, and k, both in N:...If j is quantitatively unequal to k, then qj + qk is qualitatively unequal to qx for any x in N.
§9. For every j and k, both in N:...qk x qj....=....qj + qk+j.

-- and by one or more applications of the ‘Organonic Algebraic Method’ to ‘‘‘re-solve-for’’’ any once-known but no-longer-known /-remembered terms, when the meanings of some of them are forgotten subsequent to reading this essay.

If we take the ‘‘‘replacement rate’’’ -- the percent-ratio of the count of the number of terms replaced to that of the symbolic elements so replacing -- as a crude metric for the degree of ‘semantic compression’, or of ‘knowledge-representation-condensation’, achieved, then the ‘semantic density’ improvements that we are achieving by using the stripped down, dialectical, Dyadic Seldon Function formulations, are impressive, viz. --

· out to R# and its «aporia», N^(2^5):...............32/4...=...........8 =............800% ‘semantic condensation rate’;
· out to C# and its «aporia», N^(2^6):................64/4...=........16 =.......1,600% ‘semantic condensation rate’;
· out to H# and its «aporia», N^(2^7):.............128/4...=........32 =.......3,200% ‘semantic condensation rate’;
· out to O# and its «aporia», N^(2^8):.............256/4...=........64 =.......6,400% ‘semantic condensation rate’;
· out to K# and its «aporia», N^(2^9):.............512/4...=......128 =...12,800% ‘semantic condensation rate’;
· out to G# and its «aporia», N^(2^10):...1,024/5...~.......204...=..20,400% ‘semantic condensation rate’;
· out to X# and its «aporia», N^(2^11):...2,048/5...~.......410...=...41,000% ‘semantic condensation rate’;

Using the ‘minimalized’ Seldon Function format -- a^(n^s) -- the systematic(s) core of a discourse: of a whole lecture, or of a whole text -- paper, essay, book, multi-«buch»/multi-volume treatise, etc. ... -- can be mnemonically summarized, using as few as four symbolic elements, in an expression which, with the application of three rules, & of the ‘organonic method’, if needed, can, at will, be quickly reconstituted into a series/sum/cumulum of tens, or hundreds, or thousands,... of terms, capturing, in systematically-ordered detail, the gist of the content of that discourse.

That ‘minimalized’ Seldon Function format can formulate condensed, ‘re-implicitized’, ‘connotationally curtailed’, or ‘darkened’, ‘‘‘black [w]holes’’’ of information, from which ‘‘‘white [w]holes’’’ of outpouring ‘‘‘[w]holistic’’’/mnemonic re-elaboration and reconstitution of that information are ever ready to be ‘re-unfolded’, to be ‘re-unfurled’, to be ‘rotely’ ‘re-burgeoned’, by those who know the 3 axiomatic rules [and the ‘organonic method’].

The mere assertion of a category, within a specific, interpreted progression/sum, or ‘[ac]cumulum’, of categories, is not, in itself, the delineation and articulation, or ‘explicitization’, of the detailed content -- of the progression/sum/cumulum of sub-categories and of sub-sub-categories... which are implicit in that category when it is asserted as an unarticluated, undelineated, undivided, univocal whole.

But the assertion of that undivided category does serve as a collective name for, and as a reminder of -- an intimation of -- the content of that category in its more fully articulated detail, as experienced/conducted in the past, and as still ‘rememberable’, to some degree, by the user, presently.

Of course, in the last analysis, the ‘categorogram’ or ‘category ideogram’ symbols, that constitute these dialectical progression expressions, are “intensional symbols”, not “extensional symbols”. Each is a ‘connotogram’, not an explicit list of symbols in 1-to-1 correspondence with “every last” element of meaning of the [ideo-]ontological category that it represents.

The meanings of those ‘categorograms’ are not “all there in the symbols”, and such they never can be. What each is, is a ‘mnemonic trigger’, an ‘associational catalyst’, to remind the user of, and to help [re-]evoke in the user, the rich totality of ‘implicit semanticities’ that these “intensional” symbols intend.

The richer the web of associations, of previously constructed and ‘re-member-éd’ knowledge -- of remembered experience in general -- that the user brings to those symbols, evoked in the user’s past, and retained in mind, i.e., in the user’s ‘meme-ory’, ever since, the richer, then, the totality of meanings that these ‘semantically densified’ and ‘semantically concentrated’ symbols ‘‘‘hold’’’ for that user, and the better the odds for that user to evoke that richness in and for others."



Enjoy Part II.!

Regards,

Miguel