‘The Ockhamian
Systematic Dialectic of The Sciences,
c. 1323
C.E., EXTENDED
--
‘Dialectogram’:
‘Dyadic Seldon Function Extended Ockhamian Dialectic of The Sciences.
Dear
Reader,
The case
of the Philosophical
Domain of the late Medieval, Ockhamian, Dualistic classification of The Sciences, propounded circa 1323 C.E.,
may also count as yet another case of possibly inadvertent
dialectical ‘content-structure’
in the work
of a philosopher -- in this case, in the work of a medieval philosopher whose views still register within
the modern “Philosophy of Science”.
This hypothesis of inadvertence must, however, confront the fact of the widespread exposure of philosophers of
Ockham’s time
and clime to ancient philosophical views regarding dialectic -- most
prominently, to the views
thereupon of
Plato and, especially,
of Aristotle -- a
fact which may cast some doubt upon this hypothesis, especially if, as in some still-extant
traditions, "dialectic" is restricted to the moment of opposition, or of
antithesis, between two related terms.
The medieval philosopher William of Ockham, circa 1323
C.E., developed a binary taxonomy of the sciences, rooted
ultimately in a binary ‘taxonomy of words’, one that harks back
to ancient Stoic philosophies of language.
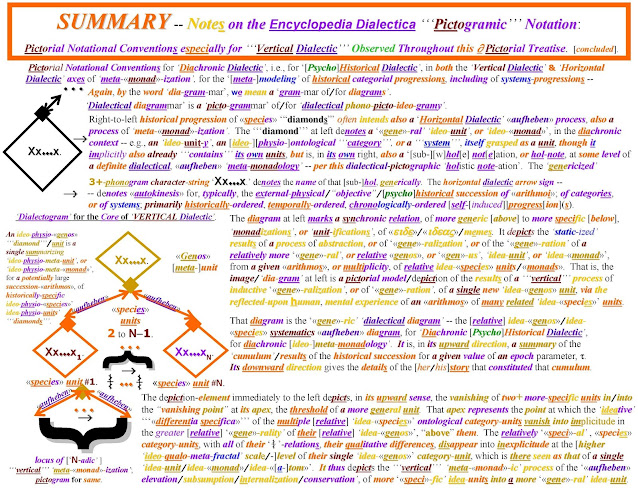
The purpose of the ‘dialectogram’ below is to note how the
formulation of Ockham’s taxonomies in a ‘meta-equation’, via the NQ
dialectical ideography,
as a systematic-dialectical ‘ideo-ontological’
categorial progression, when it is iterated one step beyond the 2
categories of science posited by Ockham, yields what we solve
herein as a ‘pre-construction’, or ‘‘‘prediction’’’, of the ‘meta-science’
species of ‘‘‘Psychohistory’’’, Y,
via two sub-species of that species, a species of
science that is still only nascent, and only ‘fractionally present’ today.
Regarding Ockham’s philosophical taxonomy of the sciences,
W. L. Reese wrote as follows*: “Ockham
makes an important distinction between categorematic and syncategorematic
terms. Most common nouns are categorematic,
while words such as “not”, “all,” and “some” are syn-categorematic.”
“...Terms that refer to things are called terms of first
intention. Terms referring to terms
of first intention are called terms of second intention‡.”
“In one sense the syncategorematic terms mentioned above are
second intentional; but, as Ockham wishes to use the distinction, categorematic
terms and syncategorematic terms, functioning together [F.E.D.: i.e., forming sentences/propositions],
refer to things. “All men are mortal” is
thus first intentional. But when we use
terms such as “genus,” “species,” and “difference” we are using terms of second
intention [F.E.D.: e.g., to form propositions of
second intention]. Propositions
utilizing such terms refer not to the world, but to terms [and to propositions -- F.E.D.] of first intention.”
“...On the basis of the distinction just mentioned, Ockham
divides the sciences into two types. Scientia
rationalis, or rational science, is second intentional. Logic is a science of this type. Scientia Realis is first
intentional. Physics is an example of a
science of real things.” *[W. L. Reese,
Dictionary of Philosophy and Religion, Humanities Press,
NJ: 1980]. ‡[cf.
George Boole on “primary” vs. “secondary” propositions, in George Boole, ...Laws
of Thought..., NY: Dover
Publications, 1958, pp. 52-53].
Suppose we denote the category for the world of real
things by r.
Suppose further that we solve for r2 as
r + t,
with t
denoting the category of “terms”.
That is, assert [‘|-’] the definition [‘=’] of the qrr in --
r2 = r(r) = r of r
= r + Delta(r) =
r + qrr as connoting t:
The r critique of r
itself as comprehending the entire known present Domain of real things =
r + Delta(r) =
r + qrr
|-=
r + t.
If so, then t implies the presence of human[oid], self-and-other-aware,
language-capable “things” -- “things”
that have, from long ago, arisen
via the brains-localized ‘self-reflexion’, the
‘self-involution’ [cf. Chardin], the bending
[‘flex’] back [‘re’] upon itself [‘self’] of the ‘pre-self-aware’
world of real things,
r,
so that parts
of the thereby-resulting ‘things-world’ ‘‘‘contain’’’ , in however distorted and omissive a way, “all” of it, if only via terms /language.
¿What,
then, happens if we, again, “square”;
if we, this time, square the result
of our earlier
squaring?
This: (r + t)2
= the (r + t) critique of (r + t) = r + t
+ qtr +
qtt.
¿What if
we solve for qtr in (r + t)2
= r + t + qtr +
qtt
as connoting the comprehension, explanation, mental appropriation, or mental assimilation
of the ‘things-world’ by terms -- by language; by human collective “universal labor”; by the collective human mind, as
merged into ‘the human Phenome’?
Then
the «arithmos» of all “true” [scientific consensus] propositions /terms
about real things forms the “extension”
which represents the “intension” of the sciences of real
things,
» Ockham’s ‘‘‘«Scientia ReaLis»’’’.
We may also denote this ‘‘‘«Scientia ReaLis»’’’ by L, such
that L stands for the «arithmos»/category
of the propositions “of first intention”, that constitute the ‘‘‘«Scientia ReaLis»’’’.
If we then decide to solve for qtt
in (r + t)2 = r
+ t + qtr + qtt as connoting the
self-comprehension, self-explanation, mental self-appropriation,
or mental self-assimilation
of the ‘terms-world’
by terms themselves, i.e.,
by language;
by human collective “universal labor”;
by the collective human mind, merged into ‘the
human Phenome’, what next results?
This: The «arithmos» of all “true” [scientific
consensus] propositions about propositions; terms about terms, as found,
e.g., in logic
and mathematics,
forms the “extension” which represents the “intension”
of the sciences “of second intention”, »
Ockham’s ‘‘‘«Scientia RatioNalis»’’’.
We may also denote this ‘‘‘«Scientia RatioNalis»’’’ by N,
standing for that «arithmos»/category of such
propositions as its units.
In sum, we have thus solved as follows --
(r + t)2 = r
+ t + qtr + qtt |-= r + t +
L + N.
In the first image pasted-in below, the ‘dialectogram’ image, we extend Ockham’s binary, dualistic
taxonomy of the sciences, by ‘re-«arché»-izing on qtr,
solved-for as L, and by then squaring L, thus generating The L critique of L itself as comprehending the entire known present Domain of the Sciences --
L2
= L(L) = L of L
= L + Delta(L) =
L + qLL |-=
L + N
-- i.e., so as to net-generate
qLL,
which we
solve for/define as N, and
which we identify
with the fourth term, qtt, in (r + t)2
= r + t + qtr +
qtt. We then again square, but this time we square
(L + N),
to obtain --
(L + N)2
|-=
L + N
+ N(L) + N(N) |-=
L + N
+ qNL+ qNN.
In the context of the foregoing ‘meta-equation’,
we
solve for the net result of N(L), namely qNL -- the ratioNal
analysis/comprehension/assimilation of the system
of propositions set forth by the sciences of the ‘‘‘«Scientia ReaLis»’’’ -- as connoting that portion of the still nascent ‘meta-science’
of ‘‘‘Psychohistory’’’,
Y, whose propositions
seek, critically, to explain the differences, the strife, the
oppositions, including the ideological aspects,
among the theories of the L sciences.
Likewise,
we
solve for the net result of N(N), namely qNN, the ratioNal
analysis/-comprehension/assimilation of the system
of propositions set forth by the sciences of the ‘‘‘«Scientia RatioNalis »’’’, as connoting that portion of
the ‘meta-science’ of ‘‘‘Psychohistory’’’,
Y, whose propositions
seek, critically, to explain the differences, the strife, the
oppositions, including the ideological aspects,
among the theories of the N sciences.
If we solve for/define ‘‘‘Psychohistory’’’ as a
whole, denoted by Y,
as the ‘‘‘sum’’’ of net N(L) and net N(N) --
(N(L) - L) + (N(N)
- N) = (L + qNL - L) + (N + qNN - N) = qNL + qNN |-=
Y1 + Y2 |-= Y
-- Then what Y comes to stand for includes immanent critiques of
ideology within the
sciences in general; within all of the
sciences -- an ‘ideo-ontological’ innovation that was pioneered by Karl
Marx, in his four-volume treatise Capital, A
Critique of Political Economy.
In our view, the meaning of qLL must extend beyond the nature of formal logic, including formal mathematical logic, to include projects
like that of Hegel’s Science of Logic, whether or not one holds that Hegel’s Science
of Logic succeeded in fulfilling such a project. Each proposition-unit in L that invokes a given universal category
becomes a sub-unit
in that unit
of N that defines that universal
category as the intension of the entire extension of L propositions that invoke/use/refer
to that universal category.
We therefore adopt the words of
Tony Smith, and of Hegel, as quoted in the second image pasted-in below, to
explicate why it is that we assert [‘|-’] N to be the correct definition [‘=’] for qLL in --
L2
= L(L) = L of L
= L + Delta(L) =
L + qLL |-=
L + N --
with qLL connoting the [propositional] self-reflexion
of the L sciences upon themselves.
If our solution of (L + N)2
=
L + N
+ qNL+ qNN is coherent, it should also suggest a
meaningful solution for all of the terms in, including the new terms
in --
(r + t +
L + N)2 = r + t +
L + N + qNr+ qNt + qNL+ qNN.
We will leave the explication of our
solutions for those new terms, qNr and qNt, for
another, later venue, leaving the
problem, for now, in the hands of you, our readers. Hint: qNt has something to do with the ratioNal,
scientific analysis of, and “accounting for”, the terms of “natural
languages”, and qNr with the ratioNal, scientific
analysis and explanation of our
perceptions
of “real”
[esp. of physical] things.
FYI: Much of the work
of Karl Seldon, and of his collaborators, including work by “yours truly”, is
available for your
free-of-charge download via --
Regards,
Miguel Detonacciones,
Member, Foundation Encyclopedia Dialectica
[F.E.D.],
Officer, F.E.D.
Office of Public Liaison