[Note: The algebraic notation used in this blog-entry may be lost or denatured in automatically-emailed summaries of it].
Dear Reader,
Introduction. The F.E.D. “first dialectical arithmetic” is [also] a dialectical symbolic logic, whose algebra serves as a first [i.e., as a simplest, most abstract, least determinate in expressive capability] algebra for dialectical logic.
This F.E.D. algebra for dialectical logic [a]mends the original, Boolean algebra for [syllogistic formal] logic, at its very root: it [a]mends the key flaw in Boole’s “Fundamental Law of Thought”, which Boole expressed – in his 1847 work “The Mathematical Analysis of Logic”, and, again, in his 1854 work “The Laws of Thought”, as explicated below.
Boole used x as an algebraic variable, or algebraic “unknown”, standing for a generic class or category – standing for any class or category – and wrote his “Fundamental Law of Thought” as a universal assertion of the reduction of “logical nonlinearity” [e.g., second [or higher] degree or power] to “logical linearity” [first degree or first power]: for every category, x –
x^2 equals x^1
-- or --
x squared equals x
-- or simply --
xx = x.
The Boolean versions of the numbers ‘0’ and ‘1’ conform to this “law”: 0 × 0 = 0; 1 × 1 = 1.
Boole’s law thus captures only a purely external version of the conservation “moment” – only the first “moment” of the dialectical «aufheben» operation, which dialectical logic asserts to be the universal operation of nature-process, including of human[oid] mind-process.
The other two “moments” or aspects of the dialectical «aufheben» operation are transformation, meaning qualitative, determinate change or determinate negation, and elevation [in level/scale of existence].
The F.E.D. “Fundamental Law of Dialectical Thought”, “Fundamental Law of Dialectical Logic”, or [just] “Fundamental Law of Dialectical Process”, [a]mends Boole’s law as follows.
F.E.D. uses x as an algebraic variable, or “algebraic unknown”, standing for a generic ontological class or category – standing for any primary “kind-of-being” class or category – as an «aufheben» [self- or other-]operation, or operator.
Note Tony Smith’s definition of a “category” in his 1990 work “The Logic of Marx’s Capital”, in which he describes the systematic dialectical logic employed by Marx to construct his «magnum opus»:
“. . . consider what a category is. It is a principle (a universal) for unifying a manifold of some sort or other (different individuals, or particulars). A category thus articulates a structure with two poles, a pole of unity and a pole of differences”. [p. 5].
That is, the meaning of a category, as standing for an “assemblage” or “set” or “population” of individuals, “contains” both the unity-moment, the aspect of what those individuals have in common, the similarity that they all share, and also, equally, the differences-moment, the aspect of the dis-similarities – the individual differences – that “differentiate”, “distinguish”, and “divide” each individual “in” a category from all others “in” its same class or category.
Given that context, F.E.D. writes their “Fundamental Law of Dialectics” as a universal assertion that “logical nonlinearity” does not reduce to “logical linearity”; that, on the contrary, “logical nonlinearity” makes a qualitative difference: for every primary ontological category, x --
x squared is qualitatively unequal to x
-- or --
xx = x + delta_x
-- or --
xx = x + qxx
-- such that delta_x or qxx represents a category or class that is qualitatively different from that for which x stands, by way of an «aufheben» conservation/transformation/elevation of the individuals for which x stands, and specifically, such that delta_x or qxx stands for a new ontological category, representing for a different category or class -- a different kind of individuals than those for which x stands.
F.E.D.’s “Fundamental Law of Dialectical Thought” is a “strong contrary” to Boole’s “Fundamental Law of Thought”.
A “weak contrary” to Boole’s law would be –
“x squared is quantitatively unequal to x”, e.g., “x squared is greater than x”, which works for all “Whole Numbers” other than 0 and 1.
That is, F.E.D.’s “law” requires ‘dialectical meta-numbers’ whose squaring or second power generates a value which is not even within the same “number-line” as its linear or first power; a nonlinear or second power value which resides in a different perpendicular direction – in a different dimension – from its first or linear power. F.E.D. has discovered such “meta-numbers”, and has axiomatized their workings [see Blog-entry # 4 of this Blog].
In general, x ---> xx = x + qxx expresses an abstracted, simplified, purely-qualitative description of what is in reality a “quanto-qualitative” dialectical process of “quantitative change leading to / becoming / turning into qualitative change”.
What is the general meaning and import of the F.E.D. Fundamental Law of Dialectics? It is a general assertion of the ubiquity of "ontological dynamics" -- of "onto-dynamasis". It is the assertion that, whenever [the "cumulum" of] a given spectrum of ontological possibilities operates upon itself, an expanded ["cumulum", representing an expanded] spectrum of ontological possibilities results.
For example, if we “apply” x to stand for a cosmological population of atoms, a, and qaa to stand for a cosmological population of molecules, also denoted by m, then –
a ---> aa = a + qaa = a + m
-- describes a cosmological new-ontology-generating process in which the expanded self-reproduction of the population-quantity of atoms, together with self-increase of the measure of their quantitative “density”, i.e., of their physical-spatial “concentration”, leads to a growing frequency and intensity of interactions between/among atoms – also presented as an “intra-action” within the population of atoms, or as a “self-interaction” of the category “atoms” – denoted by aa – which reaches a critical threshold, or “metafinite resonance singularity”, whereafter it gives rise, not only, possibly, to further increases in its own population-quantity, and quantitative density, but possibly also to a new kind of population of a new kind of “individuals” – molecules.
This description implies that qaa = m because molecules are the result of a self-«aufheben» operation of atoms upon atoms: each molecule is “meta-atom”, made up out of, and “internalizing”, a typically heterogeneous multiplicity of atoms. Each molecule thus represents an «aufheben» conservation / transformation / elevation of a sub-population of [“former”] atoms-only self-organizations.
Thus a "qaa" means a "meta-atom", or "atom of the second degree", made up out of a typically heterogeneous multiplicity of "atoms of the first degree".
Therefore, while the Boolean x operator -- x grasped as a [potential] operation upon itself, or upon other Boolean operators/operations -- is only a "preservation" operation, omitting the other two aspects of the full «aufheben» conservation / transformation / elevation operation, on the contrary, the F.E.D. x operation -- x gasped as a [potential] operation upon itself, or upon other dialectical-logic classes-or-categories-as-operators/-operations -- represents a full «aufheben» conservation / transformation / elevation operation, under the interpretation that qxx denotes a "meta-«arithmos»" relative to the qx or x «arithmos», that is, that qxx denotes an «arithmos» each of whose «monads» is a "meta-«monad»-ization", or a "meta-unit-ization", of the «monads» of the qx or x «arithmos».
Motivation: Historical Context and Application. It may assist comprehension and conceptualization of the full import and meaning of F.E.D.’s “Fundamental Law of Dialectical Process” -- a simple deductive demonstration of which is presented below -- if we locate that “Law” within the tide of human history – placing it in context within the development of the human phenome, of the “memes pool”, of the “psychohistorical material[ity]” of human history, and of the historical labor of the self-production of humanity.
In the language of the ancient Mediterranean original awakening of [Occidental] philosophy and science -- in the language of the original philosophy of mathematics, which both predates, and continues beyond, the time of Plato –
An «arithmos» is an assemblage of qualitative units – a “population” of individuals of a given kind: a “number” of individuals / individual units.
A «monad» is a qualitative unit.
If we inwardly form a mental abstraction – an idealized object, or mental object – representing such a qualitative unit, or qualitative «monad», in general, then, by referencing assemblages of such generic unit, or generic «monad», idea-objects -- anciently named, by Plato, the «arithmoi monadikoi», the mental “assemblages”, or groups/populations, of ‘mentalized’, or generic, «monads»: abstract, idealized mental “numbers” of abstract, idealized, mental «monads» / units -- then we can construct an «arithmetiké», or «arithmoi»-«techné» -- a universal “«arithmos»-art” [“art” of “number”], a universal “«arithmos»-craft” [“craft” of “number”], or a universal “«arithmos»-tech” [“technique” or “technology” of “number”]: “theoretical arithmetic”.
Diophantus of Alexandria, the father of algebra, in his «circa» 250 C.E. proto-algebraic manuscript entitled “The Arithmetica” -- or the «Arithmetiké» in transliterated Greek – actually “abbreviatively” symbolized the generic «Monadikos», or abstract qualitative unit, long before the advent of the Hindu’s abstract purely-quantitative unit symbol, 1, by the abbreviation Mo [actually, the Greek capital letter “Mu” with the lower-case letter omicron, o, written atop it], so that he symbolized our modern 1 + 1 = 2 by something more like a’Mo & a’Mo = b’Mo [the ancient Mediterranean Greek/Hellenistic civilization used “primed” letters of the Greek alphabet as numerals: «Gematria» or «Isopsephy»], not just by a’ & a’ = b’ as would later, more abstract notations such as our own, reflecting our modern, far deeper phenomic immersion in the “meme-etic” paradigm of what Marx called “The Elementary Form of [Commodity[-Capital-]]Value”, that is, in the core capital-relation consequence of the [mostly unconscious] “law of [capital-]value”, first fully raised into widespread human consciousness as such by Marx.
Motivation: Historical Context and Application. It may assist comprehension and conceptualization of the full import and meaning of F.E.D.’s “Fundamental Law of Dialectical Process” -- a simple deductive demonstration of which is presented below -- if we locate that “Law” within the tide of human history – placing it in context within the development of the human phenome, of the “memes pool”, of the “psychohistorical material[ity]” of human history, and of the historical labor of the self-production of humanity.
In the language of the ancient Mediterranean original awakening of [Occidental] philosophy and science -- in the language of the original philosophy of mathematics, which both predates, and continues beyond, the time of Plato –
An «arithmos» is an assemblage of qualitative units – a “population” of individuals of a given kind: a “number” of individuals / individual units.
A «monad» is a qualitative unit.
If we inwardly form a mental abstraction – an idealized object, or mental object – representing such a qualitative unit, or qualitative «monad», in general, then, by referencing assemblages of such generic unit, or generic «monad», idea-objects -- anciently named, by Plato, the «arithmoi monadikoi», the mental “assemblages”, or groups/populations, of ‘mentalized’, or generic, «monads»: abstract, idealized mental “numbers” of abstract, idealized, mental «monads» / units -- then we can construct an «arithmetiké», or «arithmoi»-«techné» -- a universal “«arithmos»-art” [“art” of “number”], a universal “«arithmos»-craft” [“craft” of “number”], or a universal “«arithmos»-tech” [“technique” or “technology” of “number”]: “theoretical arithmetic”.
Diophantus of Alexandria, the father of algebra, in his «circa» 250 C.E. proto-algebraic manuscript entitled “The Arithmetica” -- or the «Arithmetiké» in transliterated Greek – actually “abbreviatively” symbolized the generic «Monadikos», or abstract qualitative unit, long before the advent of the Hindu’s abstract purely-quantitative unit symbol, 1, by the abbreviation Mo [actually, the Greek capital letter “Mu” with the lower-case letter omicron, o, written atop it], so that he symbolized our modern 1 + 1 = 2 by something more like a’Mo & a’Mo = b’Mo [the ancient Mediterranean Greek/Hellenistic civilization used “primed” letters of the Greek alphabet as numerals: «Gematria» or «Isopsephy»], not just by a’ & a’ = b’ as would later, more abstract notations such as our own, reflecting our modern, far deeper phenomic immersion in the “meme-etic” paradigm of what Marx called “The Elementary Form of [Commodity[-Capital-]]Value”, that is, in the core capital-relation consequence of the [mostly unconscious] “law of [capital-]value”, first fully raised into widespread human consciousness as such by Marx.
Our earlier example, in the introductory section above, concerned a cosmological population, or «arithmos», of atom units: a “number” of atoms – e.g., a galactic interstellar “atomic cloud”, soon to transform itself into a proto-stellar “molecular cloud”.
Unlike Boole’s “primary” algebra for [formal] logic -- as his “existential logic”, “existence logic”, or “logic of things” -- in which aa = a, the F.E.D. algebra for dialectic does not get stuck in stasis –
a ---> aa = a + qaa = a + m
-- or –
“atomic cloud” ---> [goes to”, or, in time, “becomes”] “molecular cloud”.
That is, once sufficiently expandedly self-reproduced quantitatively – once “number-ous” or “numerous” enough, or “populous” enough, and “densified” enough -- the atoms in the “atomic cloud” give rise to molecules as well, that is, to a qualitatively-expanded reproduction; to the irruption of the new “cosmo-ontology”; to that new kind of being, that we call molecules.
The atoms no longer conduce to mere quantitative change, within a qualitative “onto-stasis”, but to qualitative change in the form of “onto-dynamasis”: to the irruption of a new, “molecules” ontology, or kind of being, where there once was only the atoms kind of being [ + its predecessor kinds].
The thus self-transformed, proto-stellar “molecular cloud” is an [“evolute”] “cumulum” of [at least] two ontologies; a “cumulum” of both the type a and the type m “kinds of being” --
“atomic cloud” = . . .+ a;
“molecular cloud” = . . .+ a + m.
The Boolean “Fundamental Law”, xx = x, the law of eternal simple reproduction, is insufficient to construct a more scientific science, a more empirically faithful science, a science that more fully “follows nature”.
To achieve the latter science – Marxian, dialectical science, the positive fruition of the dialectical, immanent critique of [mostly] unconsciously ideology-vitiated capitalist science – we need a[n a]mended “Fundamental Law”, the “Law” of the qualitatively/ontologically self-expanding self-reproduction of universe ontology –
x ---> xx = x + qxx
-- or --
qx ---> qx × qx = qx + qxx.
Juxtaposing the two “laws” – the Boolean and the “contra-Boolean” --
xx = x
-- versus –
xx = x + qxx
-- highlights how the F.E.D. “Fundamental Law” still [externally] «aufheben»-contains and [partially] retains the Boolean “Fundamental Law”, in the first term of the RHS of the F.E.D. law’s equation --
xx = x . . .
-- but how it also goes beyond that Boolean law, to [internally] «aufheben»-conserve, [internally] «aufheben»-elevate, and to qualitatively-transform, determinately-change, or «aufheben»-negate that “Boolean” term, x, via the second term of the RHS of the F.E.D. law’s equation --
xx = . . . qxx
-- which “double-contains” x , as xx, at the sub-script level of its generic ideographical symbol, qxx.
Thus, «in toto», the F.E.D. “Fundamental Law of Dialectical Thought” is a full-«aufheben» containment/conservation, qualitative transformation / determinate negation, and elevation [to a new scope/scale/level], of the “Boolean” term, of the x term – the “operand” or “argument” upon which x itself again, but this time as “function” or “operator – operates, or “functions” in –
x(x) = x + delta_x = x + qxx
--- and, indeed, the F.E.D. rule is the positive fruition of a dialectical, immanent critique of the Boolean “law”, of “Boole’s Rule”, as expressed in the first triad of the Dialectic of the Algebras for Logic which we explicated in an earlier blog-entry [wherein WE_ denotes the axioms-system of the Boolean arithmetic for logic, wherein WQ_ denotes the Whole numbers-based version – whose number-space is W = { 0, 1, 2, 3, . . .} -- of the axioms-system of the F.E.D. “First Dialectical Arithmetic”, and wherein WqQE_ denotes the axioms-system of the dialectical synthesis of WQ_ and WE_ ]:
WE_ ---> WE_ + WQ_ ---> WE_ + WQ_ + WqQE_.
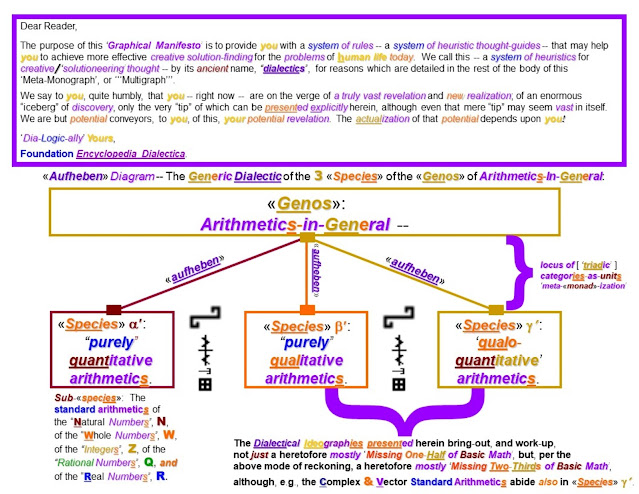
F.E.D. has identified four [qualitatively-]distinct «species» of the «genos» Dialectics in their “[Psycho]Historical Dialectic of the Dialectic Itself [a Dialectic which itself also accords with the F.E.D. “Fundamental Law of Dialectics”], all four of which have been instantiated, together, so far, historically, only in the work of Karl Marx, not [quite] in the work of Hegel, or even in that of Engels, in my view.
These four «species» are --
Systematic Dialectics & Historical Dialectics & Meta-Systematic Dialectics & Psychohistorical Dialectics.
For additional background regarding these «species», see blog-entry # 9, and/or the following definitional JPGs in the F.E.D. Glossary [ http://www.dialectics.org/dialectics/Glossary.html ] --
Systematic Dialectics --
Historical Dialectics --
Meta-Systematic Dialectics --
Psychohistorical Dialectics --
In the context of Historical Dialectics, and especially for an x which represents a physical «arithmos», or empirically-given “population” of “individuals”, the formula x^1 ---> x^2 = x + qxx is true primarily because qxx denotes an emergent phenomenon, an emergent property, an emergent quality, and an emergent ontology potential, an addition of new ontology that is already present «qua» potential, [with]in x. This is partially also the case for Psychohistorical Dialectics and for Meta-Systematic Dialectics.
In the context of Systematic Dialectics -- the Dialectics of theoretical systems as generalized, “genericized” idealizations; of “idea-objects” or “mental objects” -- where x(x) = x + qxx is a law of the “expanding reproduction” of ideas, and, especially, for an x which represents a mental-only «arithmos», such as N, or W, i.e., an abstractly-given “population” of “internal”, “mental objects”, most remote from physical/”external” experience, existing as such only for “internal”, “mental experience”, the fundamental formula of Dialectics, x^1 ---> x^2 = x + qxx, is true primarily because the category/concept/idea denoted by qxx is semantically, conceptually implicit [with]in -- is already present as a “presupposition” [with]in – x, but requires mental reflection [“self-dialogue”, or “intra-mind dialogue”], or inter-personal dialogue [“inter-mind dialogue”], to become explicit; to be “lifted up’, or “elevated”, into “explicitude”. This is partially also the case for Meta-Systematic Dialectics and for Psychohistorical Dialectics.
As with a holographic image, or hologram, in which each part of the whole image contains a “sided”, “tendentious”, “distorted”, “deformed”, “fuzzy” replica of that whole image, such that the image as a whole, as “made up out of its parts”, is, in this sense, “made up out of itself”, so it is also with a well-developed, matured theory, or conceptual system. That is, such a theory-system is “holonomic”, meaning that each of its category/concept parts “contains” – entails / involves / presupposes -- all of the other category/concepts of that system implicitly. This “implicitude” can be evoked, or “out-voked”, into “explicitude”, via introspective reflection, or via inter-personal [“Socratic”] dialogue, or via skillful oral, or written, “monologue-ic” presentation.
The pedagogical strategy of Systematic Dialectics , as a dialectical method of totality-theories presentation, is to start with/from the simplest, most abstract of the categories/concepts in this “holonomic” network of mutually-involved, “inter-pre-supposing”, “intergenerate” categories/concepts, as «arché» / beginning, and to proceed from there, evoking a[n ever-lengthening] series of more complex, more “thought-concrete” [more “determinate”; more richly «speci»-fied] categories/concepts, as successor series, from each predecessor series, -- from each less lengthy, less complex, less “thought-concrete”, series -- until the most lengthy series, ending with the most-complex, most-“thought-concrete” category/concept -- one which most richly in-itself represents the total human experience of the [sub-]totality of human experience so theorized -- is reached / presented / evoked.
Demonstration. A Simple Deductive Proof of the F.E.D. “Fundamental Law of Dialectical Thought” from the Axioms of the NQ_ axioms-system of Dialectical Arithmetic.
Given: n is an element of the set N = { 1, 2, 3, . . .} of "Natural" Numbers.
To Prove: x "times" x is qualitatively unequal to x,
for every x in NQ = { q1, q2, q3, . . .}, the set of the F.E.D. "First Dialectical Meta-Numbers".
Proved:
Assertion
#......................Assertion Content_____________________.......Assertion Justification
1......................n is an element of N......................................................Given
2......................qn is an element of NQ, for every n in N..............Axiom 5
3.....................qn squared = qn + q2n, for every n in N.........Axiom 9
4.....................n does not equal 2n, for every n in N................*
5......................qn is qualitatively unequal to q2n,
............................for every n in N...............................................................Axiom 6
6.......................qn + q2n is qualitatively unequal to qn,
.............................for every n in N..............................................................Axiom 8
7.......................qn may be represented by x,
.............................for any n in N.................................................................Equivalent Substitution
8........................x squared is qualitatively unequal to x..............Assertion # 3 &
............................................................................................................................Assertion # 6, above:
............................................................................................................................Q.E.D.
*The proposition "n does not equal 2n, for every n in N." is justifiable, for example, from a corollary of a theorem of the "Natural Numbers" axiomatic system of arithmetic that derives from the "multiplicative identity element" axiom for that system. This theorem asserts that for any element of the set of "Natural Numbers", call it m, that is not the "multiplicative identity element" of that set, and for any element of the set of "Natural Numbers", call it x, it is true that x < mx.
Here is the same theorem again, but this time expressed in something closer to the "full regalia" Encyclopedia Dialectica notation --
Key Upshot: The “contra-Boolean” F.E.D. “Fundamental Law of Dialectical Thought” is not a direct premise, assumption, presumption, postulate, or axiom of the NQ_ axiomatic system of arithmetic for dialectical algebra: it is a proven theorem of that system.
The proof above invokes the following Axioms of the NQ_ axiomatic system of arithmetic for dialectical algebra, posted previously to this Blog, in blog-entry # 4 [with some new commentary included] --
“Dear Reader,
Thought it might be useful to reproduce here the core "axioms" -- the main rules -- of the "rules-system", or "axioms-system" ["axiomatic system"] of the F.E.D. "First Dialectical Arithmetic".
. . .
Axiom 5. For every n in N, qn is in NQ.
[this states the «aufheben» tie between the N and the NQ. The rest of the rules below state "Non-Standard" aspects of the NQ relative to the "Standard" N].
Axiom 6. For any j and k, both in N:
If j is quantitatively unequal to k, then qj is qualitatively unequal to qk.
[This axiom expands the "trichotomy principle" of the "Standard" arithmetics -- the principle that for any arithmetical objects a and b, just one of the following three relations obtains:
a < b, or a = b, or a > b
-- to a "tetrachotomy principle", that adds a fourth possibility, that of qualitative inequality, to the basic possible relations between any pair of arithmetical objects].
. . .
Axiom 8. For all j, and k, both in N:
If j is quantitatively unequal to k, then
qj + qk is qualitatively unequal to qx
for any x in N.
[This is the rule that makes dialectically interpreted NQ expressions "ontologically anti-reductionist". It means that a "heterogeneous sum" of ontological categories, like C + M in the previous blog-entry, does not reduce or collapse into any single ontological category at the same level of generalization as its summands. This rule too is crucial to the calculations summarized in that previous blog-entry.
Another way of understanding this axiom is to say that it denies "additive closure" for the arithmetic of the NQ.
Addition is not a "closed" operation for the NQ.
Indeed, every addition of a pair of [qualitatively-]distinct NQ 'dialectical meta-numbers' leaps beyond the NQ space of 'dialectical meta-numbers'. Every such addition operation jumps you to a "place", to a value, that is outside of the set NQ.
As the next axiom shows, by way of re-expressing 'dialectical multiplication', i.e., '«aufheben» multiplication', or 'ontological multiplication', in terms of 'dialectical addition', i.e., of 'non-reductionist/qualitative addition', the NQ 'dialectical meta-numbers' form a 'comprehensively OPEN' arithmetic.
That is, the NQ 'meta-numbers' arithmetic is NOT CLOSED for either of the operations that these axioms define for it.
Any addition operation for distinct 'dialectical meta-numbers', and any multiplication operation among these 'dialectical numbers' at all, distinct or not, gives rise to 'diagonal transcendence'.
Any such operation thus represents, generically, an 'ontological revolution'.
This means that any such operation gives rise to a value which corresponds to a 'meta-diagonal' directed line-segment in the '''analytical-geometric representation''' of the NQ '''set''', or "space", i.e., to a directed line-segment, 'meta-vector', or 'dialector,' which '"transcends"', or resides beyond, that set of the non-diagonal 'dialectors' which forms the '"space"' of the NQ.
For illustrations regarding this point, see --
http://www.dialectics.info/dialectics/Dialectic_Ideography_files/6_Dialectics-Part1c-Briefing_OCR.pdf
-- pages I-147; I-152.].
Axiom 9. For every j and k, both in N:
[qk] x [qj] = [qj] + [q(k+j)].
[This rule is most crucial of all to the "purely-qualitative, algorithmic calculations" presented in the previous blog-entry. It defines what "multiplication" means among the NQ "dialectical meta-numbers". It is called, by F.E.D., "the double-conservation «aufheben» evolute product rule".]
. . .”
Regards,
Miguel









No comments:
Post a Comment