
A new introduction to F.E.D.'s historic discovery of algebraic dialectical logic has just been posted to the www.dialectics.info website, written by a non-member student of that website, who has produced an 8-page overview of the F.E.D. discovery that may be more accessible than anything ever written by F.E.D., or -- I am sorry to admit -- by me [so far].
See --
http://www.dialectics.info/dialectics/Briefs.html
http://www.dialectics.info/dialectics/Briefs_files/Joy-to-You,%20Toward%20Understanding%20%27%27A%20Dialectical%20Theory%20of%20Everything%27%27,%2004JUN2012,%20as%20posted.pdf
Here it is, rendered into the fonts available to this blog-entry --
"Toward Understanding “A Dialectical Theory of Everything”
A General Summary of Theory, Purpose, Application
About this document: a self-tutorial
Since my teen years, this mathematician/human has sought a way to give mathematical structure to ideas, concepts, beliefs, etc., under a “more humane way of thinking/acting” (a better “logic”). Soon after discovering “A Dialectical Theory of Everything,” I recognized its depth and beauty, its comprehensiveness and applications, and its potential to assist in Mankind’s growth, especially in the peaceful ways sought / mandated by its founders. This theory provided an “Answer” to my search, and this model has become a real Joy to me (as it may be to You).
In seeking to understand the theory and application from all the information provided, I began this document as an attempt to clarify the concepts to myself and any interested others (perhaps via a website). This document is an independent effort, dedicated to providing information about this new worldview, in language that, I hope, speaks to a wide audience.
The worldview, or dialectical model, that has been developed by Foundation Encyclopedia Dialectica [see About F.E.D. section below], might be called a “Dialectical Theory of Everything” in that it encompasses virtually every aspect of our Universe: cosmological natural history as a whole, including human history, science, philosophy, etc. The Foundation’s stated goal is to communicate this model/methodology through various channels, and to encourage its application. This document is an attempt to serve that goal, in ways the author deems appropriate.
As a basis for “self-tutorial,” the Background and Summary/Item sections below are intended to give the reader (or student) sufficient grounding in the theory so as to be able to continue his/her own research/use of the model. Only after understanding the Summary/Items [1-12], do I recommend accessing the guideline URL’s (indicated by [Ref-xx]) given in the [References] section below. The [Quick Primer] section at the end may also aid the reader “come up to speed” quickly with the key concepts of the theory.
Note: This author (not F.E.D.) is solely responsible for any “errors of understanding” in presenting the theory.
About F.E.D.
F.E.D., or Foundation Encyclopedia Dialectica, is a private, independent organization, established for the purpose of developing methodologies which may greatly assist HumanKind, in terms of both human survival and human flourishing. Its stated goal is to communicate these methodologies through various channels, and to encourage their application to understanding / resolving a vast variety of human and scientific issues.
Towards this goal, F.E.D. extends an “Omni-Copyright” to anyone seeking to use its methodologies, and also refuses to accept any “profit” (in financial terms, or in terms of intellectual credit, etc.) or “outside gifts” in return for its efforts, other than the revenues from sales of its books/media to cover its production costs. Much of the F.E.D. literature is available for free download from two websites. [Ref Z]
Note: F.E.D. has offered interpretations of its models, including some which have economic and political implications, resulting in its advocacy of views/beliefs on how best to proceed economically and politically. These views are not explored here, since this document is dedicated to explaining this new methodology and to encouraging its use, without bias.
Background
The dialectical model stems from F.E.D.’s intensive and extensive research into human thought and history, especially that of the ancient Greek philosophers Heraclitus, Pythagoras and Plato.
The latter two valued the role of “Number,” not only in its widely-understood quantitative sense, but in a qualitative sense in which a “different kind of number” reflects universal ideas and the [self-]interactions of those ideas. The mutual and self-interaction of such “quality numbers” or “qualifiers” on themselves produces a qualitative expansion of the universe of ideas as its natural effect. This self-repeated [self-]interaction (dialectic) is seen as responsible for all growth and progress.
A dialectical process is “self-correcting” in that its results are continually fed back into itself and re-adjusted / re-evaluated. Plato’s contention is that real knowledge can be obtained, and sustained, only by continual dialogue / dialectic.
Most crucially to me, this theory goes beyond the Boolean logic of true/false, i.e. a logic which preserves the current system (when that system S interacts with itself): S x S = S, and which implies only “all or nothing” like possibilities: {1, 0}.
In essence, any system based on Boolean logic can’t lead us to any Newness (S x S = S) beyond its Oldness (S). It represents a narrow true/false logic that is great for designing airplanes and electrical circuits, but not-so-great for showing us how to “think out of that ‘Old’ [0/1] box!” Needed is a “contra-Boolean logic” to show us how to think/act in a richer, more inclusive way! And this is what the F.E.D. model provides and helps us to do.
In this spirit of dialog and a more-inclusive way, this theory/model is offered for your consideration and use.
Terminology Used
F.E.D. has developed its own language: Special technical terms and other neologisms for communicating (describing) the worldview embodied in its model. Such terms are often “dense with meaning,” and are meant to convey both etymological history as well as a healthy interplay of ideas. It is through such “neologisms” that new, deeper meaning is conveyed. [This document will use these neologisms only where they are essential to convey meaning that cannot otherwise be conveyed.]
If the reader finds the terms difficult [when viewing F.E.D. documents], we recommend that he/she patiently “glance over” such terms – reading for the real content expressed or implied. Your patience will most likely be rewarded with a truly new and remarkable worldview! [Ref-T]
Example: As a contraction of “event” and “entity”, the term “eventity” is used (perhaps first by Prof. Archie J. Bahm in his 1976 book, Polarity, Dialectic and Organicity). This use is not meant to be cute, but rather to convey how process (verb) and subject/object (noun) can be thought of as one “eventity” which possesses subject-verb-object relationships, thereby suggesting/defining a new manner of perceiving and/or thinking.
Summary: A Brief Look at the Model
Out of a concern regarding the limitations of the existing discourse and progress in which mankind is presently engaged, F.E.D. has documented (critiqued) several issues in our existing mathematics, science, philosophy, history, politics, economics, etc., that it contends constitute a “barrier” to the further progress that it considers desirable. [Ref-S1]
Its critique in this regard constitutes not an “external” one, based upon criteria which are foreign to those fields, but a dialectical one, i.e., an “immanent” critique,” a critique internal to a given system’s own self-view, that leads to the self-view of a richer system, as in what the Foundation calls “The Goedelian Dialectic”. [Ref-S2]
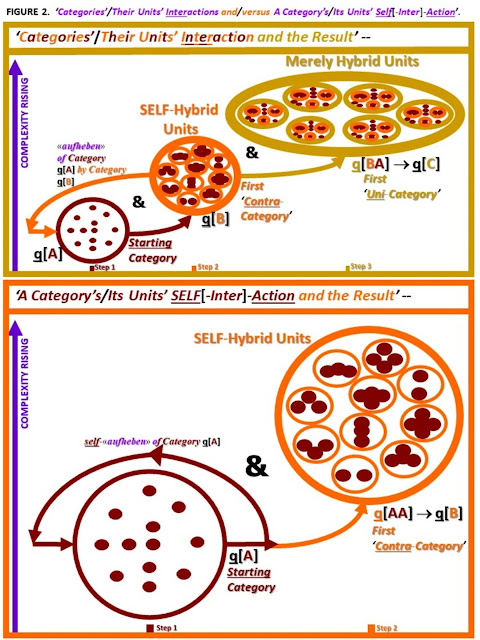
Having carefully researched the philosophies of the ancient Greeks, et al., the theory’s founders have resurrected Plato’s principle of dialog and dialectic, and have rediscovered a form of his “idea numbers”. More recently, the dialectic principles offered by the “early modern” German philosopher G. W. F. Hegel (early 1800s) suggest that a given Thesis gives rise to its AntiThesis, which together interact to form a SynThesis, which then constitutes a NewThesis on the next-richer level of concreteness. [Such “levels” are referred to as “fractal scales”.] Hegel further mentions an «aufheben» process by which the original thesis/idea is not only 1) “conserved”, 2) “negated, canceled, or annulled”, but also 3) “elevated” into a new resulting thesis. These principles serve as the basis for the model, which has been rigorously mathematically-formulated in F.E.D. publications, and is interpreted below. [Ref-S3]
Summary Items (1-12):
1. The Fundamental Equation of the Dialectic: Qualitatively [Self-]Expanding Universes of Discourse
The model first considers a given initial finite set or system, S0, based upon a “Universe of Discourse”, or initial “Universal Set” of [non-set] “logical elements”, U ( S0 = 2^U, the “set of all subsets” of U ), and the notion of S0 interacting with itself (“dialoguing with itself”, if you will). This interaction is defined by a “multiplication” (x) operation as S0 x S0 ( S0 “of” S0 ).
Under the dialectic principle, this S0(S0) product is not only the same system 2^U = S0 again, but that system S0 plus a key added qualitative, ontological increment to that system: delta(S0), forming the new system: S1 = S0 + delta(S0).
Thus, the Fundamental Equation of the Dialectic for any growth-stage (“epoch” t) is:
St+1 := St x St = St + delta(St).
Thus, Boolean logic (represented by S x S = S) is “conserved” via the St term of “St + delta(St)”, but that “logic of St” is also “annulled” and “elevated” by the delta(St) term.
The reconciliation of Old (St) and the implied Newness (delta(St)) is accomplished in their sum: St + delta(St)”, which represents the New system (St+1).
[This reconciliation process employs Hegel’s
Thesis x AntiThesis = Thesis + AntiThesis + SynThesis
notion and his general aufheben process.]
The underlined St signifies a “quality number”, i.e., it exhibits the “trans-Boolean” characteristic (S x S = S + delta(S), where delta(S) is not null), while the underlined delta(St) signifies a qualitative increment -- an increment of ontology (“kind of being”) of a new kind –- but still derived from the initial S0 = 2^U. [Ref-01]
2. New Kinds of Numbers to Model Expanding Ontologies
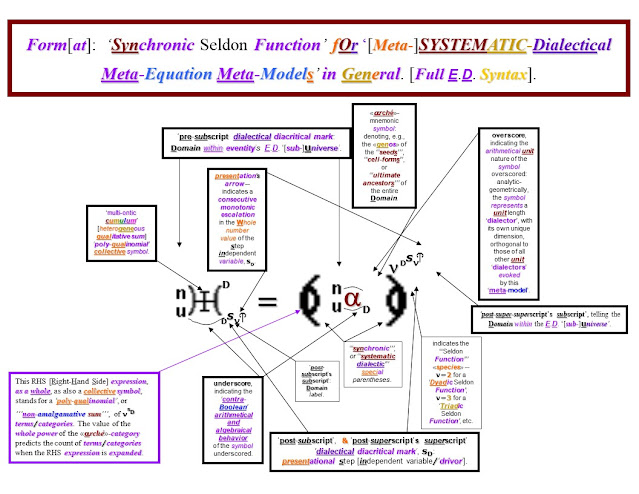
Here, the words “ontology” or “ontological” refer to “kinds of being.” In order to capture or contain “the (ontological) qualities or ideas of such an expanding universe of discourse”, a new set of “generalized numbers” is postulated by F.E.D. Such numbers are referred to as “ontological qualifiers”, or as “quality numbers” by this author. The set or space of such qualifiers is:
NQ := { q1, q2, q3, …},
Each such qualifier behaves more like a “set of qualities/ideas/beliefs/etc.” rather than like a single “element of a given quality”. Just as N is a general set of symbols that can be applied to quantities of any specific kind of object (e.g., apples), NQ is a general set of symbols that can be applied to the defining quality (ontology) of any specific kind of object, or subject of discourse (e.g., qualities of/ideas of/beliefs about apples). [Ref-02]
3. Name for these new numbers: The Meta-Natural Meta-Numbers
Because these “quality numbers” correspond to the Natural Numbers but are beyond them in that they account for qualitative matters only, NQ is referred to as the space of Meta-Natural Meta-Numbers.
Notes: Plato’s term «Arithmoi Eidetikoi» literally translates as “Numbers of Idea Units”, wherein «Arithmoi» translates as “Assemblages” [of qualitative Ideas-as-Units]. Therefore, “quality numbers” represents this author’s attempt to capture this meaning. [Ref-03]
4. These New Kinds of Numbers are “Purely-Qualitative”(unaddible)
Since adding the same quality to itself does not change that quality (as in set-union), each such qualifier has this simple “non-additive property”:
qn + qn := qn for any qn in NQ
Note: F.E.D. asserts an order principle for the NQ, and a “total order relation” for the NQ sequence, a sequence of increasing qualitative determinateness (here q3 represents greater qualitative “determinateness” than q2, which represents greater qualitative “determinateness” than q1).
5. The Additive/Multiplicative “Open-ness” of “Open Qualifier Space”
In NQ, the sum of any two different qualifiers is not another qualifier within the set NQ. Likewise, the product of any two NQ qualifiers is not in NQ. In the case of either operation, the result goes outside of – beyond – the NQ space. There is no compelling need for “closure of addition,” nor for “closure of multiplication”. Thus, with the NQ number system, an “operationally open system” of arithmetic emerges. In short, NQ keeps us in “pure idea space” (or “Meta-Natural ontologies space”) exclusively, without worry as to its “closure of ideas”. This openness “creates room” (at every stage) for qualitative, ontological increments of new ideas to emerge from the interactions among already existing ideas! This open space, I call “Open Qualifier Space”. [Ref-05]
Note: “Open Qualifier Space” is somewhat analogous to the Natural Numbers under division: The resulting “open system” produces a different kind of set, the Fractions (Rational Numbers), which is a qualitatively different set from the set of the “whole” Natural numbers. Thus, in Open Qualifier Space, whenever an idea-sum occurs, we can qualitatively, connotatively [“intension-ally”] “interpret it”, rather than definitively [“extension-ally”] “define it”. Such “openness” will be desirable when interpreting the resulting mathematical findings that express “expansions of idea ontology”, or “expansions of physical ontology”.
6. Ontological Multiplication
Again, the words “ontology or ontological” refer to “kinds of being” – the “kinds of physical things” and “kinds of ideas” that actually exist in any given epoch t (the “t” of the St). The dialectic principle is also reflected by the non-commutative multiplication (“´” interaction) of such “ontological qualifiers” in NQ as defined by:
qm “of” qn: qm x qn := qn + qn+m
qn “of” qm: qn x qm := qm + qm+n
This definition reflects Hegel’s «aufheben» process [Quick Primer section]. [Ref-06]
7. Arithmetic to model “The Goedelian Dialectic”
In this model, “a [transient] closure of resulting ideas” is implied via a dialectic and interpretation of the resulting products/sums. An important result of logician Kurt Goedel’s completeness/incompleteness theorems of the 1930s is:
If an existing system cannot solve a problem that arises within it, then that system can be expanded to form a larger system in which that problem can be solved.
That larger system will also allow the formulation of new problems, which did not exist for its predecessor systems, but which both exist for it, and which are unsolvable within it, thus giving rise to additional system enlargement, and so on.
This continual process of enlargement Goedel famously termed “the inexhaustibility of mathematics.”
Thus, the F.E.D. model also embodies a “Goedelian dialectic,” which allows a system to expand qualitatively and “idea ontologically” so that it can solve any of the problems which arise within any of its predecessor systems, but still not some of the problems which arise within it (the new system) for the first time. [Ref-07]
8. Arithmetic to model the “Autokinesis” of the “Set of All Sets”: delta as “qualo-operator” on St
The expansion increment delta(St) was discussed earlier for a “universe-of-discourse” or “universal set” U such that S0 = 2^U.
But exactly what is this increment?
In general, this increment is defined to be all the subsets of St (i.e., “all combinations generated by elements within St”), denoted as 2^St.
Thus, “delta” is itself a quality-function, or “qualo-operator” on quality set St, which together create delta(St), the power set of St.
So, initially, delta(S0) = 2^S0 which helps define the next epoch’s (t = 1) “set of all discourse”:
S1 = S0 “union” 2^S0.
[The delta(S0) = 2^S0 can be large or small, depending on the nature of the problem(s) to be solved].
delta(St) := the “set of all subsets of St” := 2^St,
which, when combined with the set for time epoch t, namely St, then forms the new system/discourse set St+1 for the new period (epoch t+1).
Thus, this general set-content expansion formula serves as the Fundamental Equation of the Dialectic:
St+1 = St union 2^St,
or
St+1 = St + delta(St),
as originally mentioned in Item 1.
Each new “t” represents an attempt to complete the system by obtaining the “set of all sets” (all discourse universes), which can never fully be attained (completed), as explained in the Note below. [Ref-08]
Note: This “set of all sets” movement, which is the “extensional” definition of the concept of a “set” itself, is not the result of any external need for content-expansion, but of an “internal” need for such expansion.
It is a “self-movement”, or “Autokinesis”.
As given in its very name – “the set of ALL sets” – its nature drives its content-expansion (via the delta(__) = “power set” operator), which is therefore a “SELF-expansion”. Any set St always excludes all of its own subsets, including its “improper” subset – itself – so it fails to be “the set of ALL sets”.
The move to “ St ‘union’ 2^St ” puts the missing sets, 2^St, “back” into St, but that changes St into a new, qualitatively different, qualitatively expanded set, named St+1, which, again, fails to be “the set of ALL sets”.
The qualitatively new subsets that are added in each “try” at the “set of all sets”, St, represent the “extensions” of progressively ever more subtle qualities, represented by the elements of 2^St.
9. “Meta-Linearity” of “Qualitative Sums”
The Dialectic Equation is saying (assuming) that any ontological value/quality/discourse set St, interacting with, or reflecting upon, itself, yields itself again, but also plus some “delta”, representing a solution set which “solves” old problems, or creates new “possibilities”, in the t+1 epoch (via set St+1). Thus, the Equation always expresses the
St x St = St^2
product as a linear “sum”, or “union”, of qualitatively unequal sets, of “apples” + “oranges” + “pears” + … . This process “[meta-]linearizes” the “nonlinear [squaring] interaction,” St x St = St^2, into a “qualitative sum”,
St + delta(St),
which serves as the basis for the “self-iterative” algorithm behind F.E.D.’s Mathematics of Dialectics.
The prefix ‘meta-’ is used because this linearity is at/on the “level of addition of ontological qualifiers”, rather than on “the level of addition of pure, unqualified quantifiers”. [Ref-09]
10. Breaking through “The Nonlinearity Barrier”
As the Dialectic Equation indicates, the (ontological) product is a linear sum of qualifiers, and this points toward an answer to -- or breakthrough of -- the “Nonlinearity Barrier” which plagues present-day modern science. [Ref-10]
11. Connotational Calculus with an Algorithmic Underpinning
To become specific to a given universe of discourse, the (F.E.D.) dialectical model requires “interpretations” (“assignments”) of the new ontology expansion terms (the delta terms) that result from repeated interaction (multiplication) of the previously-posited sums of ontological qualifiers. It is these interpretations which can make-or-break any such dialectical model’s results in the non-science sphere of discourse. [Ref-11]
12. New Method for Hypothesis-Discovery in the Sciences
However, when this F.E.D. Dialectic approach is applied to “subjects of scientific discourse”, it results in a sweeping new understanding of Science, e.g., from subatomic particles to atoms to molecules, etc. It also results in a new universal taxonomy of the “fractal” layers of … sub-«species» to «species» to «genos» to super-«genos» …, etc. (ontological categories), thereby dramatically re-organizing our knowledge of the ontology of the cosmos! All this emerges from successive application “epochs” of the F.E.D. dialectical, “self-iterative” algorithm – rather appropriately called: "A Dialectical Theory of Everything". [Ref-12]
[References] Links to greater detail on each item or topic
Below are URL references to F.E.D. publications which explain each above concept in detail, in “F.E.D. terminology”.
We recommend that these URLs be used for self-tutorial only after becoming thoroughly familiar with the Background and Summary/Item sections of this document.
The reason these links are not placed directly where they are first referenced is: The tutorial asks that the student engage in a conscious “going to the link”, rather than almost unconsciously clicking on the link immediately after reading the summary item.
Unless the viewer attains a good “Overview” understanding first, “clicking on a link” will open him/her to greater detail than is recommended. Thus, the general and tutorial presentation philosophy of this site/document is:
“See the forest first, understand “the lay of its land,” then study the trees in as much detail as you wish using the “links” provided below.
Also, the reader may wish to study the last section [Quick Primer] on the Math of Dialectics before accessing the links below.
[Ref-T]:
http://point-of-departure.org/Point-Of-Departure/ClarificationsArchive/Eventity/Eventity.htm
[Ref-S1]:
http://www.adventures-in-dialectics.org/Adventures-In-Dialectics/DiaRith/Intro/Dialectical-Ideography_An-Introductory-Letter.htm#The_Nonlinearity_Barrier
[Ref-S2]:
http://www.adventures-in-dialectics.org/Adventures-In-Dialectics/DiaRith/Intro/Dialectical-Ideography_An-Introductory-Letter.htm#Example_0
[Ref-S3]:
http://www.dialectics.info/dialectics/Correspondence_files/Letter17-06JUN2009.pdf
[Ref-01]: Pages 111 through 112 at
http://www.dialectics.info/dialectics/Dialectic_Ideography_files/7_Dialectics-Part1c-MetaBrief_OCR.pdf
[Ref-02]: Page I-141 at
http://www.dialectics.info/dialectics/Dialectic_Ideography_files/6_Dialectics-Part1c-Briefing_OCR.pdf
[Ref-03]:Pages I-6 through I-10 at
http://www.dialectics.info/dialectics/Briefs_files/_Brief2-29JUL2008_OCR.pdf
and
http://www.adventures-in-dialectics.org/Adventures-In-Dialectics/DiaRith/Intro/Dialectical-Ideography_An-Introductory-Letter.htm#The_Dialectic_According_to_Plato
and
http://www.dialectics.info/dialectics/Glossary_files/F.E.D.,%20A%20Dialectical%20%27%27Theory%20of%20Everything%27%27,%20Volume%200.,%20FOUNDATIONS,%20Edition%201.00,%20first%20published%2010DEC2011,%20last%20updated%2017AUG2011,%20Definition,%20ARCHE%27,%20JPEG_1.jpg
[Ref-04]: Page 111 at
http://www.dialectics.info/dialectics/Dialectic_Ideography_files/7_Dialectics-Part1c-MetaBrief_OCR.pdf
[Ref-05]: Page I-148 at
http://www.dialectics.info/dialectics/Dialectic_Ideography_files/6_Dialectics-Part1c-Briefing_OCR.pdf
[Ref-06]: Page I-145 at
http://www.dialectics.info/dialectics/Dialectic_Ideography_files/6_Dialectics-Part1c-Briefing_OCR.pdf
[Ref-07]:
http://www.adventures-in-dialectics.org/Adventures-In-Dialectics/DiaRith/Intro/Dialectical-Ideography_An-Introductory-Letter.htm#Example_0
[Ref-08]:
http://www.adventures-in-dialectics.org/Adventures-In-Dialectics/DiaRith/Intro/Dialectical-Ideography_An-Introductory-Letter.htm#The_Dialectic_of_Set_Theory
[Ref-09]:
http://www.adventures-in-dialectics.org/Adventures-In-Dialectics/DiaRith/Intro/Dialectical-Ideography_An-Introductory-Letter.htm#An_Ideography_for_Example_5
[Ref-10]:
http://www.dialectics.info/dialectics/Correspondence_files/Letter24-22JFEB2010.pdf
[Ref-11]: Page 1 at
http://www.dialectics.info/dialectics/Briefs_files/_Brief1-29JUL2008_OCR.pdf
[Ref-12]: Pages B-7 through B-37 at
http://www.dialectics.info/dialectics/Primer_files/4_F.E.D.%20Intro.%20Letter,%20Supplement%20B-1,%20v.2_OCR.pdf
[Ref-Z]: Two websites offering F.E.D. texts for free download are --
www.dialectics.info (includes blogs and outside correspondence)
and
www.adventures-in-dialectics.org (includes blogs and detailed documents presenting F.E.D. concepts)
[Quick Primer] on the Math of Dialectics
This section is an attempt to provide a quick background on the math of dialectics, as currently understood by this author: a) the “Meta-Naturals” set of increasing ontologies, NQ := { q1, q2, …, qn }, b) the ontological multiplication of elements in this set, and c) some applications of the theory.
In N := {1, 2, 3, …}, <1+> “n times” generates any n, but (1x) generates only itself.
In NQ, <q1 +> generates only itself, but quite significantly, <q1 x> “n-times” generates the “n-th Cumulum”, Cn := (q1)^n = q1 + q2 + … + qn.
Using this result, it is possible to show an “isomorphic” correspondence between the Naturals (under +) and “Cumula space” (as I call it) under multiplication (x) of cumula.
Let h(n) := (q1)^n := Cn, then Cn x Cm = Cn+m, or h(n+m) = (q1)^(n+m) = (q1)^n x (q1)^m = h(n) x h(m), which makes h(n) = (q1)^n, quite analogous to “exp(n) = e^n” in the Reals: e^(n+m) = e^n x e^m, and the “Cum” or “Sum” notion is analogous to “Integration” (in the Reals) as Note’d below [for WQ & ZQ, s.t. W := {0, 1, 2, …} & Z := {…, -2, -1, ±0, +1, +2, …}], in the advanced “Special Note”.
Special Note: In one key sense, “q1” is like a “qualitative e”, where e^x := exp(x) quantitatively!
Map h: W ---> { WQ Cumula }, where h(w) = (q1)^w = Cw means that the cumulum “sum[marize]s all ontologies from q0 to qw”.
This seems analogous to integrating the quantitative function “exp(x)” over the interval [0, n] (epochs 0 to n), where [using 'S' as the sign for the integration operation -- M.D.] Sexp(x)dx [from t = 0 to n] “sums up” (is the “cumulative result” of) all historical (exponential) growth during those epochs!
So, “In sum”, on [t = 0, n], in quantitative space: e^n = e^0 + S(e^t)dt;
in qualitative space: (q1)^n = (q1)^0 + SUM(t=0,n)qt, with SUM signing non-amalgamative summing, and given that, for ZQ space, (q1)^0 = (q1/q1) = q-1 x q+1 = (q0/q1) x (q1/q0) = q1^(-1) x q1^(+1) = q1^(-1+1) = -q1 x +q1 = q0 = q-1 + q+1 + q+1-1 = q0 + q0 = q0, by the more symmetric, ‘meta-genealogical product rule’:
qz1 x qz2 := qz1 + qz2 + qz2+z1,
for z1, z2 in Z.
Interestingly, NQ is neither closed under + nor x.
Any qn + qn = qn, but when m is not n, qn + qm is NOT in NQ, since these are “unaddible numbers” (Plato) or “non-amalgamative” sums (Musès), i.e., ontologies don’t really mix.
Instead one is usually “subsumed” by another, as the defined multiplication indicates:
qm “of” qn := qm x qn := qn + qn+m.
Any universe of sets 2^U = S0 (ontology) acting on itself under an Hegelian (and Goedelian) Dialectic is said to obey the Fundamental Equation of the Dialectic ( “the F.E.D.”
St+1 := St x St = St + delta(St), or
Snew := Snow x Snow = Snow + delta(Snow).
The delta(Snow) also represents the “power set” of Snow, which represents a new framework or possibilities for solutions to problems within Snow that are not solvable within Snow.
Snow union delta(Snow), or “Snow + delta(Snow)”, represents including Goedel’s next higher “logical type”, which permits solution of the unsolvable problem in Snow.
Thus, “delta” is itself a quality-function, or “qualo-operator”, on quality set St, which together create delta(St), the power set of St.
So, delta(St) := the “set of all subsets of St” = 2^St.
The “+” represents a “meta-linear” addition (to the next/subsuming ontological level of “epoch t”).
This is a “linearization” of S x S that embryonically solves the “Non-Linearity Barrier”, which the Foundation contends is an obstacle to growth not only in Science, but to growth in our Civilization in general.
Under Boolean logic in “Quantitative” space, S x S = S, with no non-zero delta term, and our solution set is only the Boolean possibilities: {0, 1} since S(1 - S) = 0.
In essence, Boolean logic represents a narrow true/false logic that is great for designing airplanes and electrical circuits, but not-so-great for showing us how to “think out of that [0/1] box!” We need a “contra-Boolean logic” to show us how to think in a richer, more inclusive way!
With the delta increment or “operator on the ontology (St)” in open “Qualifier” space, this non-zero increment yields a “contra-Boolean” solution set, thus posits a “contra-Boolean logic”.
Note: By way of contrast, in Lawlor’s book, Sacred Geometry, he mentions the equation for the Golden Mean: x^2 = x + 1, where that Mean (“reconcilor”) is seen as a kind of universal growth factor. There, only a constant “positive unity delta” (+1) exists, so the non-Boolean “linearized” alternative suffers from a “constant” delta(x) = 1, which in no way depends on the limitations imposed within the system (since “1” is a constant).
Thus, applying this methodology to the ontological development of math systems, we might start with S1 := q1 := {the ontology of the Natural numbers,N}, then S1 x S1 = (q1)^2 = q1 + q2, where q2 = {idea-ontology solving x + n = n} = ontologies up to the Whole Numbers, W.
Then (q1)^3 = q1 x (q1 + q2) = C1 x C2 = C1+2 = C3 = idea-ontologies up to the Integers, Z --
(q1)^4 = q1 + q2 + q3 + q4 = C4 = idea-ontologies up the Rational Numbers, Q, etc.
The succeeding ideas-system (idea-ontology) solves what is unsolvable in the previous ideas-system (idea-ontology)!
Finally, we apply this methodology to our Quantum World of q1 = {subatomic particles physio-ontology}. Then (q1)^2 = cumulum up to {atomic particles physio-ontology}, (q1)^3 = cumulum up to {molecules physio-ontology}, etc.
Oh, one more interesting notion. Expand NQ via a q0 where q0 + qk = qk for any k in N. Then q0 = id(+), the additive identity.
And, surprisingly: q0 = id(x), the multiplicative identity, also!
This would be impossible in any non-trivial algebraic field, but is quite possible in ontological qualifier space!
That’s what I love about this space -- It lets the “Impossible” scream loudly: “I’m Possible!” And, of course, the Complex numbers were founded under a counter-thesis to the impossibility of an x (in the Reals) such that x^2 = -1. It was then that “little i” screamed: “i am!” and (happily for us all) she was heard."
Regards,
Miguel
Miguel










Dear Readers,
ReplyDeleteThe "pseudonymous" author of the introduction quoted in the blog-entry above, Joy-to-You, wrote me as follows --
"Miguel,
"Toward Undetstanding ..." looks good on your blog.
You placed it into nice "bite-sized" paragraphs.
I trust others will share our enthusiasm for this useful model, and apply it to their field of endeavor.
The very notion of a dialogue or dialectic is something vitally needed in today's contentious world.
-- joy2you"
Regards,
Miguel